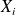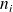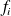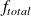Étude d'un caractère quantitatif discret
Nombre d'enfants par famille
Aidons-nous d'un exemple pour découvrir les spécificités des variables quantitatives discrètes, aussi appelées variables quantitatives discontinues :
Imaginez qu'un instituteur veuille faire des statistiques sur les nombres d'enfants dans les familles des 25 élèves de sa classe.
Le caractère étudié est le nombre d'enfants par famille. C'est une variable quantitative qui peut être 1, 2, 3, ... mais pas 1,5
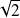ou
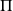. C'est donc bien une variable discrète.
Collecte des données
Voici ce qu'ont répondu les élèves : 1 3 5 1 2 2 1 1 3 4 2 3 2 4 2 1 1 3 3 5 4 2 1 2 1
Après avoir obtenu ces réponses, l'instituteur compte combien sont enfants uniques (8), combien sont deux enfants dans la famille (7), combien trois (5), etc.
Il dispose ces comptes dans les deux premières colonnes d'un tableau.
La première colonne contient le caractère étudié : le nombre d'enfants par famille. Cette liste est ordonnée de 1 à 5.
La seconde colonne reprends les effectifs c'est à dire le nombre d'enfants qui ont répondu 1, 2, 3, 4 et 5.
Le total au bas de la seconde colonne est l’effectif total (25) c'est le nombre d'élèves dans la classe.
Nombre d'enfants par famille
| Nombre de familles Effectif
| Fréquence
| Fréquence cumulée croissante | fréquence cumulée décroissante |
|---|---|---|---|---|
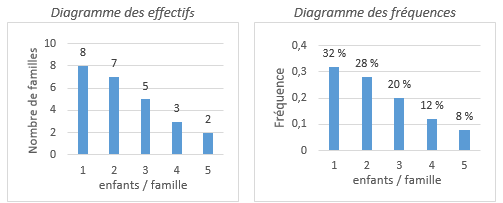
1 | 8 | 0,32 | 0,32 | 1 |
2 | 7 | 0,28 | 0,60 | 0,68 |
3 | 5 | 0,20 | 0,80 | 0,40 |
4 | 3 | 0,12 | 0,92 | 0,20 |
5 | 2 | 0,08 | 1 | 0,08 |
|
|
L'instituteur qui a quelques notions de statistiques calcule ensuite quelles sont les proportions d'enfants pour chaque réponse.
La fréquence des enfants uniques est 8/25 = 0,32.
Sept élèves sur 25 soit 28% sont deux enfants dans leurs familles, et ainsi de suite.
Les fréquences sont les rapports entre les effectifs partiels et l'effectif total.
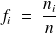
Les fréquences cumulées croissantes apporteront des réponses aux questions telles que
« Quelle portions d'élève sont moins de 3 enfants dans leur famille ? »
La fréquence cumulé d'indice
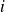se calcule en additionnant toutes les fréquences d'indice
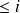
0,32 | 0,32+0,28 = 0,60 | 0,60+0,20 = 0,80 | 0,80+0,12 = 0,92 | 0,92+0,08 = 1
Les fréquences cumulées décroissantes permettent de savoir quelle est la proportion d'élève qui sont plus de
enfants chez eux.Ce cumul se calcule en additionnant toutes les fréquences en partant du bas du tableau.
0,08 | 0,08+0,12 = 0,20 | 0,20+0,20 = 0,40 | 0,40+0,28 = 0,68 | 0,68+0,32 = 1
Représentations graphiques
Les graphiques construits à partir des valeurs chiffrées des tableaux facilitent la comparaison des grandeurs mesurées en mettant en évidence leurs importances relatives.
Diagrammes en bâtonnets
Les bâtonnets disjoints montrent que les valeurs portées en abscisse sont des valeurs discontinues.
Les effectifs ou les fréquences sont portés en ordonnée et servent à la mesure des hauteurs des bâtonnets. Ils sont tous de largeur identique.
Histogramme
L'histogramme des fréquences cumulées est un diagramme en forme d'escalier. Les bâtonnets sont contigus pour mieux montrer la progression du cumul. On peut par exemple lire sur ce diagramme que
|  |
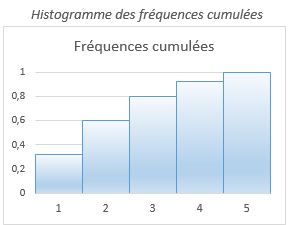Polygones des effectifs ou des fréquences
Les mesures au lieu d'être représentées par la hauteur de bâtonnets sont marquées par des points parfois reliés par des segments de droite. Ce type de diagramme convient aussi bien pour montrer les effectifs, les fréquences et les fréquences cumulées. |  |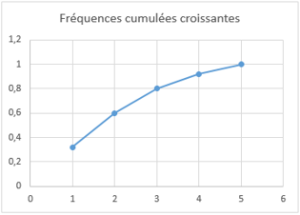
Diagrammes circulaires
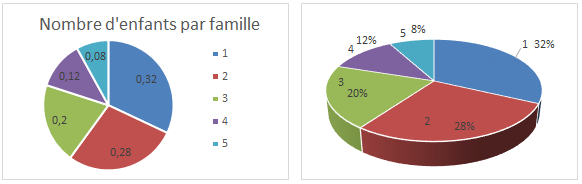
Ces diagrammes conviennent pour les effectifs et les fréquences, mais pas pour les fréquences cumulées.
Les diagrammes circulaires donnent un aperçu rapide et acceptable quand la précision n'est pas fondamentale. Il est en effet plus facile de comparer deux hauteurs de bâtonnets que deux surfaces de secteurs. Le fait que les familles de trois enfants sont plus nombreuses (12%) que celles de deux enfants (8%) est à peine visible sur ces diagrammes circulaires représentés ci-dessus alors que cette différence est flagrante sur les diagrammes en bâtonnets.
Le fait de mettre le diagramme circulaire en 3D est d'un bel effet visuel mais la perspective donne des effets trompeurs. Pour preuve : les 28% de familles de deux enfants semblent sur le diagramme de droite plus importants que les 32% de familles d'une seul enfant.
