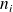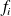Étude d'un caractère qualitatif
Collecte des données
Imaginons que l'on observe les décisions prises après une délibération pour une classe de 20 étudiants.
En consultant la liste des étudiants prise dans l'ordre alphabétiques, nous découvrons les décisions suivantes : réussi, réussi, réussi, refus, ajourné, refus, réussi, ajourné, ajourné, refus, ajourné, refus, ajourné, réussi, réussi, réussi, refus, réussi, ajourné et ajourné.
La décision est une donnée qualitative. Elle peut prendre comme valeur : réussi, ajourné ou refus.
Présentées ainsi, les informations recensées sont trop confuses. On aimerait les organiser mieux.
Les informations de réussite, d'ajournement ou de refus ne sont pas numériques mais il nous est tout de même possible de les compter.
Disposons ces valeurs et leur comptage sous forme de tableau.
Décision | Nombre d'étudiants |
|---|---|
Réussi | 8 |
Ajourné | 7 |
Refus | 5 |
Dans le jargon des statistiques, ces nombres 8, 7 et 5 sont appelés les effectifs.
Le nombre 8 est l'effectif qui a réussi, 7 est l'effectif ajourné et 5 est l'effectif refusé.
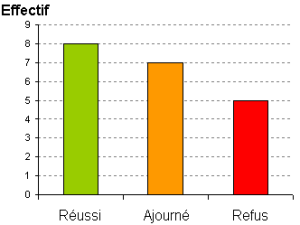
L'effectif total noté
est le nombre total des étudiants.
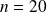
Définition : Effectif
Effectif : Nombre de personnes composant un groupe.
Exemples : L'effectif du personnel, l'effectif d'une classe.
Synonyme : nombre
Tableau des fréquences
L'analyse des décisions devient plus parlante encore si en plus de compter les effectifs on les compare à l'effectif total.
La fréquence d'un effectif est la proportion de cet effectif par rapport à l'effectif total. Cette fréquence
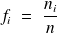est un nombre compris entre 0 et 1, elle peut aussi s'écrire en pourcents.
Le rapport entre la somme des effectifs et l'effectif total vaut 1 (100%)
Les valeurs des fréquences relatives à l'effectif total permettent les comparaisons ultérieures à d'autres classes qui n'ont pas nécessairement le même effectif.
Décision | Effectif
| Fréquence relative
| |
|---|---|---|---|
Réussi | 8 | 0,4 | 40 % |
Ajourné | 7 | 0,35 | 35 % |
Refus | 5 | 0,25 | 25 % |
Total | n = 20 | 1 | 100 % |
L'effectif total est la somme des effectifs partiels. n = 8+7+5 = 20
La fréquence est le rapport entre les effectifs partiels et l'effectif total.
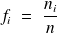
Quand ce rapport est donné en % , l'effectif total correspond alors de 100 %
Représentation graphique
Diagramme en bâtonnets
On dispose les données sur l'axe horizontal et on reporte l'effectif ou la fréquence sur l'axe vertical . Les bâtonnets sont disjoints et de largeurs identiques. Les hauteurs sont proportionnelles aux effectifs ou aux fréquences. |  |
Diagramme sectoriel
Aussi appelé diagramme circulaire ou diagramme en secteurs, et de façon plus familière « camembert » en France ou « Pie chart » en anglais.
Conviennent bien pour représenter les pourcentages à condition toutefois que le nombre de variables soit limité, sans quoi il devient illisible.
Diagramme sectoriel Réussi = 0,40 x 360° = 144° Ajourné = 0,35 x 360° = 126° Refus = 0,25 x 360° = 90° |  |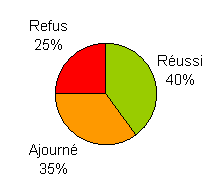
