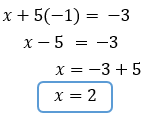Résolution par combinaison et élimination
Méthode :
Transformer une des équations pour isoler une première inconnue à gauche du signe égal.
Remplacer cette inconnue dans l'autre équation. Celle-ci ne contient plus que la seconde inconnue. Sa résolution donne la valeur de la seconde inconnue
Remplacer l'inconnue trouvée dans l'équation qui par la première transformation isolait la première inconnue.
Reprenons l'exemple du début :
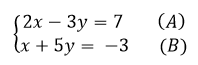
1. Les inconnues et les valeurs indépendantes sont déjà disposées de manière identique dans les deux équations. Il n'y a donc rien à changer pour la première étape.
2. Multiplions chaque membre de l'équation (B) par -2 de sorte à obtenir des coefficients opposés pour x
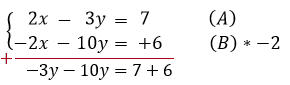
3. La somme des deux équations est une nouvelle équation à une seule inconnue, et donc facile à résoudre.
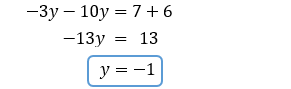
4. Remplacer l'inconnue trouvée dans une des deux équations de départ.
Prenons celle avec laquelle cela semble le plus simple, l'équation (B) dans cet exemple.