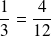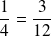Opérations arithmétiques avec les fractions
Addition et soustraction
Nous savons que l'addition et la soustraction sont des opérations qui ne peuvent se faire qu'avec des objets de même nature « On n'additionne pas des pommes et des poires ». Dans le cas des fractions on ne peut additionner ou soustraire que des fractions dont les dénominateurs sont identiques, des tiers avec d'autres tiers, des quarts avec des quarts, mais jamais des tiers et des quarts.
Exemple : Tâchons de nous représenter l'addition
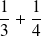
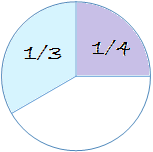 | Quelle part cela fait-il du gâteau ? Il faut d'abord subdiviser les parts à additionner, le tiers et le quart, en parts égales. |
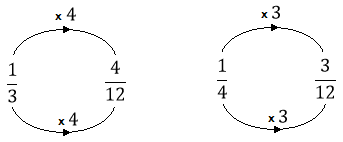
On obtient des parts identiques en divisant le tiers en quatre
et divisant le quart en trois
| 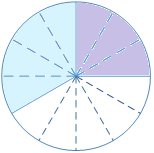 |
1/3 et 4/12 sont des fractions équivalentes. Elles représentent bien la même portion de gâteau.
Idem pour 1/4 et 3/12 .
Les subdivisions étant maintenant égales, nous pouvons compter le total en douzièmes.
 +
+
 =
=
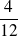 +
+
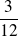 =
=
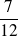
Méthode : Calcul préliminaire du dénominateur commun
La principale difficulté, avant d'additionner ou soustraire deux fractions, est donc de trouver comment transformer chaque fraction pour que toutes aient le même dénominateur.
Le dénominateur commun sera un multiple de tous les dénominateurs présents dans l'addition.
Autres exemples d'additions et de soustractions de fractions
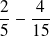 Le dénominateur commun sera 15 car 15 est à la fois un multiple de 5 et de 15.
Le dénominateur commun sera 15 car 15 est à la fois un multiple de 5 et de 15.
Le calcul devient donc :
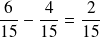
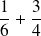 Le dénominateur commun doit être un multiple de 6 et de 4.
Le dénominateur commun doit être un multiple de 6 et de 4.
On pourrait prendre 6 * 4 = 24 mais 12 est aussi un multiplicateur de 6 et 4.
En effet 12 est commun à la table de multiplication par 6 : 6, 12, 18, 24, ... et à la table de 4 : 4, 8 , 12, ...
12 est préférable 24 car il est plus petit, les calculs seront donc plus faciles.
Le calcul devient donc :
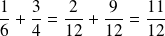
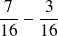 Ici le dénominateur étant identique pour chaque terme de la différence, la réduction au dénominateur commun n'est pas nécessaire.
Ici le dénominateur étant identique pour chaque terme de la différence, la réduction au dénominateur commun n'est pas nécessaire.
On peut de suite soustraire les numérateurs.
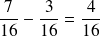 qu'on peut simplifier :
qu'on peut simplifier :
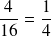
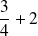 C'est le moment de se souvenir que tout nombre entier
C'est le moment de se souvenir que tout nombre entier
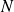 peut aussi s'écrire sous la forme d'une fraction
peut aussi s'écrire sous la forme d'une fraction
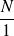
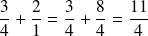
Multiplication
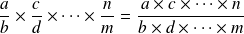
Pour multiplier des fractions, il suffit de multiplier les numérateurs entre eux pour le dessus et les dénominateurs entre eux pour le dessous.
On peut quand c'est possible procéder à des simplifications entre n'importe quel facteur du numérateur et n'importe quel autre facteur du dénominateur.
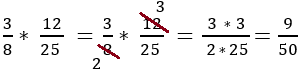
Division
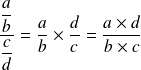
Diviser par une fraction, c'est multiplier par la fraction inverse