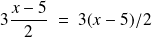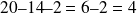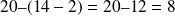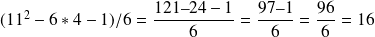Réduction des expressions algébriques
Simplifions les expressions algébriques d'allure complexe en appliquant quelques règles simples.
1° Regrouper les termes semblables
Les termes semblables sont ceux qui ont la même partie littérale.
Ex. :
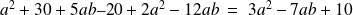
Le résultat n'est plus réductible car il ne contient plus de termes semblables
2° Supprimer des parenthèses
Simplifions les expressions littérales en supprimant les parenthèses quand c'est possible.
Exemples :

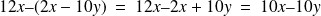
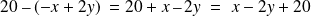
Attention :
Pour supprimer une paire de parenthèses précédée du signe moins, il faut changer le signe de tous les termes qu'elle contient.
3° Développer ou factoriser
La simplification d'une expression algébrique se fera
- tantôt en la développant, c'est à dire en la répartissant sous la forme d'une somme (un polynôme)
- tantôt en la factorisant, c'est à dire en la présentant sous la forme d'un produit.
Rappel : Règle des priorités des opérations
La règle des priorités des opérations s'applique quand il y a plusieurs opérateurs dans une expression. Cette règle précise l'ordre dans lequel doivent s'effectuer les opérations.
En présence d'opérations de même priorité, les calculs se font de gauche à droite.
|
Remarque : « Somme » et « produit »
Quand en algèbre on parle d'une somme, il s'agit d'une somme algébrique qui concerne aussi bien des valeurs positives que négatives. On parle donc à la fois d'additions et de soustractions.
Somme signifie à la fois addition et soustraction
De même, quand dans ce même contexte on parle de produit. Cela concerne aussi bien les valeurs en valeur absolue plus grandes ou plus petites que 1.
Diviser par 2 c'est multiplier par 0,5. Diviser par n, c'est multiplier par 1/n
Produit signifie à la fois multiplication et division