Expression algébrique
Une expression algébrique (ou expression littérale) est une suite d'opérations à effectuer sur des valeurs dont certaines sont représentées par des lettres.
Les lettres utilisées dans ces expressions représentent des valeurs variables ou constantes. Les premières lettres de l'alphabet a, b, c etc. sont choisies de préférence pour représenter des nombres constants (invariables) et l'usage veut que les lettres x, y et z représentent des valeurs variables, indéterminées ou inconnues. Bien que dans les applications pratiques nous préférerons des lettres plus représentatives des valeurs à symboliser , voyons pour commencer comment les mathématiciens font avec les variables qu'ils nomment habituellement
,
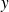et
.
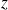Mais tout d'abord commençons par définir quelques termes utiles pour désigner les expressions algébriques et les opérations qui les concernent (Monôme, polynôme, réduire, développer et factoriser).
Définition : Monôme
Un monôme est un produit de facteurs.
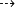"2a²bx" est un monôme.
C'est une expression algébrique qui ne contient aucun signe d'addition ou de soustraction.
Il est recommandé de ranger l'ordre des facteurs de manière à en simplifier la lecture.
Ex :
Écrivons d'abord les coefficients numériques puis la partie littérale en commençant par les constantes (a, b, ...) et en terminant par les variables (x, y, ...)
Le fait d'écrire ces lettres dans l'ordre alphabétique permet de reconnaître plus facilement les monômes semblables.
Définition : Polynôme
Un polynôme est une somme algébrique de monômes.
Exemples :
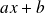est un binôme
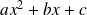est un trinôme (du second degré)
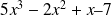est un quadrinôme (du troisième degré)
On dit d'un polynôme qu'il est du nième degré si n est le plus grand exposant trouvé pour la variable.
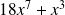est donc un polynôme du septième degré.
On s'efforcera d'ordonner les polynômes par rapport aux puissances décroissantes des variables, cela systématise et facilite les calculs.
