L'addition
Définition
L'addition numérique vise à exprimer par un seul nombre, appelé somme, la quantité que représente l'ensemble des nombres ajoutés.
L'addition de deux grandeurs physiques donne une grandeur physique de même nature qui résulte de la réunion des valeurs ajoutées.
Du point de vue numérique, l'addition est l'opération la plus élémentaire. Compter, c'est déjà additionner.
Le résultat de l'addition est appelé somme ou total
Les nombres à additionner sont appelés termes de l'addition.
Propriétés de l'addition
Commutativité
a + b = b + a
L'ordre des termes est sans importance.
Associativité
a + b + c = (a + b) + c = a + (b + c)
Les regroupements de certains termes sont possibles.
Zéro est un élément neutre pour l'addition
a + 0 = a
Ajouter zéro ne change rien.
Somme algébrique
Les nombres et les grandeurs peuvent avoir des valeurs négatives.
Ajouter une valeur négative revient à faire une soustraction.
Exemples : 18 + (-5) = 18 - 5 = 13 « Plus par moins = moins »
-5°C +7°C = 2°C Si après un gel à -5°C, la température remonte de 7°, c'est qu'il fait 2°C
Somme de grandeurs
Puisque notre but est de faire des mathématiques appliquées, considérons que les valeurs à additionner puissent être autre chose que des nombres purs sans dimensions.
Sachons faire la distinction entre « nombres abstraits » et « grandeurs » :
On écrira que 3 < 50 (3 est inférieur à 50) c'est une comparaison entre deux nombres purs, abstraits, sans dimension.
Mais 3 km > 50 cm (3 km est supérieur à 50 cm) c'est la comparaison de deux grandeurs
L'addition est une opération qui s'effectue sur des grandeurs de même espèce.
La somme est une grandeur de même nature que les termes de l'addition.
Quand par exemple on additionne deux distances ont obtient une distance, et si on additionne deux nombres sans unité le résultat est lui aussi un nombre sans unité. Quand les grandeurs à additionner, bien que de même nature sont exprimées avec des unités différentes, il suffit de les convertir dans une même unité avant de procéder à l'addition.
Exemples :
1 pouce + 10 mm = 25,4 mm + 10 mm = 35,4 mm
13h50 + 30 min = 14 h 20
Addition écrite
Placer les nombres les uns au dessus des autres en alignant les chiffres de même rang (unités, dizaines, centaines, ... ou dixièmes, centièmes etc.)
Commencer alors l'addition par la droite en marquant les reports au dessus.
Exemple :
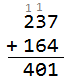 | 7+4 = 11 ; on pose 1 et on reporte 1 1+3+6 = 10 ; on pose 0 et on reporte 1 1+2+1 = 4 ; on pose 4 , la réponse est 401 |
Exercices
Calculer sans oublier de noter les unités choisies
1 km + 250 m =
5 cm + 12 mm=
2h40 + 50 min =
200 W + 4 kW =
2,5 km + 1400 m =
0,5 km + 80 m =
800 W + 2 kW =
2,4 m + 70 cm =
1,2 kg + 850 gr =
8h30 + 50 min =
12 cm + 240 mm =
Sommes algébriques

Calculs écrits
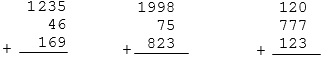
Calculez par écrit :
117,62 + 90,88 =
0,492 + 0,0795 =
Complétez les opérations suivantes :

Carrés magiques
Placez dans chacune des cases un chiffre différent de sorte que dans toutes les directions le total fasse 15. | 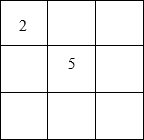 |
Complétez le tableau suivant de sorte que tous les nombres de 1 à 25 y figurent une fois et que dans toutes les directions la somme soit de 65 | 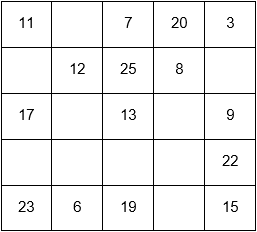 |





