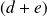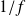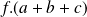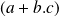Formules combinaisons de sommes et de produits
Partons d'une relation de la forme
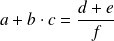
a = ?
Comment transformer
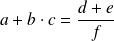pour trouver
?
dans le membre de gauche est le terme d'une somme.
Pour l'isoler il faut faire passer l'autre terme
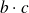de l'autre côté du signe égal.
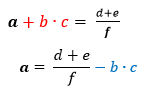
b = ?
Comment transformer
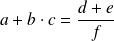pour trouver
?
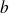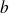est le facteur d'un produit qui est lui même le terme d'une somme.
Commençons par évacuer
le terme gênant de cette somme
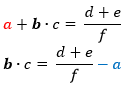
Le membre de gauche n'est plus maintenant qu'un produit.
Le facteur gênant
est un multiplicateur. Il s'inverse et devient diviseur en passant à droite.
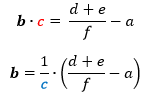
f = ?
Comment transformer
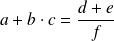pour trouver
?
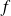Le membre de l'équation qui contient la variable à isoler est un produit. C'est le produit de
Déplaçons
Le membre de l'équation qui contient la variable à isoler est un produit.
Le facteur excédentaire
|  |
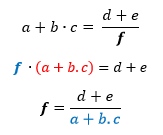e= ?
Comment transformer
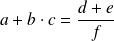pour trouver
?
Le membre de l'équation qui contient la variable à isoler est le produit de
Le diviseur f devient multiplicateur en passant de l'autre côté. Le membre de l'équation qui contient la variable à isoler est maintenant une somme. Le terme excédentaire change de signe en passant de l'autre côté. On permute les deux membres de l'équation |  |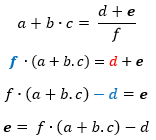
