Introduction
Vous connaissez sans doute (ou vous retrouverez facilement) la formule pour calculer une vitesse à partir d'une distance et d'un temps.
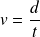
C'est une formule simple. Il suffit de savoir que la vitesse s'exprime en km/h, pour comprendre que la vitesse se calcule en divisant la distance donnée en km par la durée du trajet comptée en heures. La formule est inscrite dans les unités. « Kilomètre par heure » dit bien qu'on divise les km par des heures.
Si par contre vous connaissez la distance à parcourir et la vitesse à laquelle cette distance sera parcourue, le calcul du temps nécessaire est moins immédiat. Pourtant, entre les trois grandeurs que sont le temps, la vitesse et la distance, la relation est toujours la même. Elle est donnée par la formule
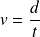 mais cette fois c'est
mais cette fois c'est
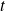 que l'on cherche.
que l'on cherche.
On va devoir transformer la formule.
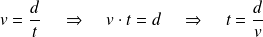
Vous pensiez connaître une formule. Mieux que cela, une relation entre trois grandeurs vous donne trois formules. A condition bien entendu de savoir transformer les formules.
Une relation entre
 grandeurs
grandeurs
 formules.
formules.
Autre aspect de la question : Notre exemple concernait une vitesse exprimée en km/h. Il arrive que l'on change d'unités. Pour passer en mètres par seconde par exemple. Ou encore pour exprimer cette vitesse en unités anglo-saxonnes ou en nœuds marins. Les changements d'unités seront vus à la fin de ce chapitre.





