Introduction
Une équation est une égalité entre deux expressions algébriques.
Elle est représentée par un signe égale placé entre les deux membres de l'équation, deux expressions algébriques dont l'une d'elles au moins contient une ou plusieurs inconnues.
« Résoudre l'équation » consiste donc à chercher la (ou les) valeur(s) de la (ou des) inconnue(s) qui vérifie(nt) cette équation.
Exemples
Les valeurs 3 et -5 vérifient-elles l'équation suivante :
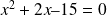
Voyons ce que donne l'équation quand on remplace
par 3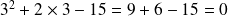
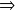3 est donc bien une solution de l'équationProcédons de même avec -5
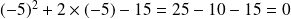
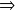-5 est donc une autre solution de cette même équation.
Testez par vous même si les valeurs 1 et -1 vérifient les équations suivantes :
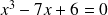
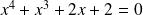
Les exemples qui précèdent nous ont montré ce que sont les solutions d'une équation. On observe que même avec une seule inconnue, certaines équations peuvent avoir plusieurs solutions. Le nombre maximum de solutions correspond au degré de l'équation c'est à dire plus grand exposant de
.
Nous verrons dans la suite du cours comment retrouver les solutions des équations en commençant par le cas le plus simple : l'équation du premier degré à une inconnue.
