Résolution des équations du premier degré à une inconnue
La résolution d'une équation nécessite des transformations successives de celle-ci tout en veillant à conserver l'égalité entre ce qu'il y a à gauche et à droite du signe égal.
Le but des transformations est d'obtenir des expressions plus simples et finalement la (ou les) valeur(s) de la (ou des) inconnue(s).
Résolvons l'équation
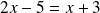en notant les opérations faites de manière identique de part et d'autre du signe égal pour isoler
à gauche.
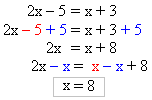
Les deux membres de l'équation ci-dessus étaient tous deux de simples sommes algébriques. On a fait passer les termes en
dans le membre de gauche et les termes indépendants dans le membre de droite.
Au final,
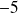est passé de gauche à droite en changeant de signe
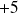
et le terme
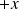à droite est devenu
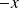en passant dans le membre de gauche.
Voyons comment résoudre cette autre équation :
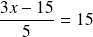
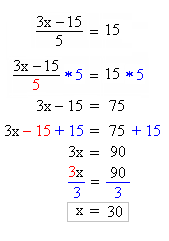
Pour aller plus vite, on n'écrit plus les "
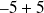" ou les "
"
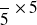Tout ce passe comme si on faisait passer les nombres d'un côté à l'autre du signe égal en changeant les opérations que font ces nombres. En passant d'un côté à l'autre du signe égal, les moins deviennent des plus, les plus deviennent des moins, les divisions deviennent des multiplications et inversement les multiplications se transforment en divisions.
L'équation est vue comme une balance que l'on veille à garder en équilibre. Toute opération faite sur le membre de gauche doit être faite identiquement sur le membre de droite. |  |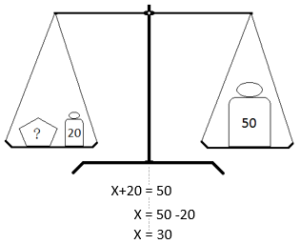
