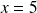Résolution des équations du second degré
Forme canonique
Quelle que soit son aspect initial, toute équation du second degré à une inconnue peut être ramenée à la forme suivante :
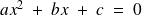
C'est ce que nous appellerons la forme canonique de l'équation. Ce n'est qu'une fois mise sous cette forme que nous envisagerons d'en chercher les solutions.
Exemple :
Supposons que l'on doive résoudre l'équation
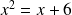
La première chose à faire est de la transformer pour la mettre sous sa forme canonique :
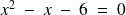
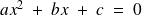
a est le coefficient du terme en
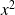, b est le coefficient du terme en
et c est le terme indépendant.
Dans l'exemple cela donne :
=1, b=-1 et c=-6
Cas général
Partons de l'équation mise sous la forme
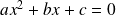avec
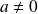
Considérons que les coefficients constants
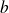et
sont eux aussi différents de 0.
La recherche des solutions passe alors nécessairement par l'utilisation de l'algorithme que voici :
Calculer le discriminant
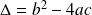
La suite passe par le calcul de
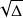, elle n'est possible que si
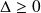
Si
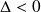
le calcul de
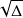est impossible et l'équation n'a aucune solution.
Sinon, puisque
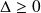le calcul de
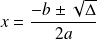est réalisable
Si
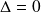
l'équation n'a qu'une seule solution
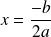
si
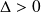, la valeur de
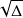est un nombre réel positif
et l'équation a alors deux solutions
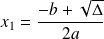et
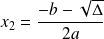
Exemple :
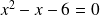
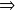
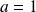
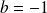
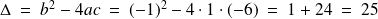
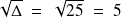
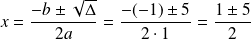
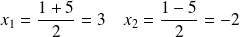
Cas particuliers
L'algorithme précédent reste valable dans tous les cas. Cependant, si b ou c valent 0, la recherche des solutions est plus simple et rapide en procédant comme suit :
Si
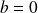, autrement dit si l'équation mise sous sa forme canonique n'a pas de terme en
L'équation devient
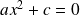
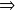
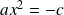
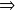
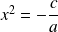et donc
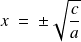
Si
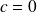, autrement dit, s'il n'y a pas de terme indépendant, par la mise en évidence de x
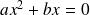devient
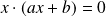
Si le produit de
par
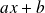vaut 0, c'est donc que s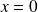oit
soit
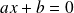
Les deux solutions possibles sont donc
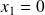et
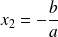
Exemple :
(
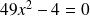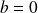, il n'y a pas de terme en x)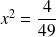
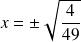
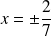
les deux solutions son t
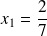et
(
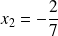
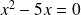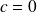, il n'y a pas de terme indépendant)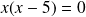
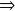Les deux solutions sont
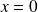et
