Règle de trois
Bien que la règle de trois soit enseignée dès l'école primaire, bon nombre de personnes restent perdues devant les problèmes de proportionnalités.
Une des façons d'enseigner la règle de trois est de construire un tableau des proportionnalités à quatre cases. Le contenu de l'une de ces quatre cases est la valeur recherchée en partant des trois valeurs connues d'où le nom de la règle. La méthode de résolution pourrait se résumer comme suit multiplier des deux valeurs connues sur une diagonale et diviser ce produit par la valeur restante.
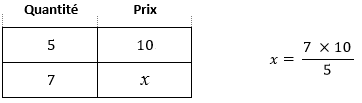
Cette méthode est une recette, un "truc" efficace lorsqu'il existe une proportionnalité directe entre deux variables comme le prix à payer en fonction de la quantité achetée, les dosages, les conversions d'unités, les questions d'échelles des plans et des cartes etc.
Le défaut de cette recette est qu'elle produit des résultats aberrants lorsqu'elle est utilisée de manière irréfléchie. Soit parce que les grandeurs considérées ne sont pas vraiment proportionnelles (comme l'âge et la pointure, la quantité d'eau tombée et la durée de la pluie), soit parce que les grandeurs au lieu d'être directement proportionnelles sont inversement proportionnelles.
Exemple : Passage par l'unité
Méfions-nous des recettes et des formules mal comprises car cela mènent à des erreurs grossières ! Place donc au raisonnement :
25 m de câble coûtent 17,50 €, combien coûtent 36 m ?
1) 25 m coûtent 17,50 €
2) 1 m coûte 25 fois moins → 17,50 / 25
3) 36 m coûtent 36 fois plus → (17,50 / 25 ) x 36
Méthode : Principe de résolution
1° Écrivez une première ligne qui exprimer le rapport qu'il y a entre deux des données.
Commencer cette première ligne en indiquant la valeur qui varie, ici la longueur ;
Puis terminer cette ligne en indiquant la valeur à recalculer, ici le prix.
2° Calculer ce que deviendrait cette valeur à droite pour une valeur unitaire à gauche.
Attention ici au sens de la proportion. Est-elle directe ou inverse ?
Si la proportion est directe, toute variation des données à gauche donne une variation identique à droite. (Si on divise à gauche il faut diviser par le même nombre à droite)
Si la proportion est inverse, toute des données à gauche donne une variation inverse à droite. (Si on divise à gauche il faut multiplier par le même nombre à droite)
3° Le rapport à une valeur unitaire étant établi, on évalue ce que devient la valeur recherchée en fonction de la modification de la troisième donnée.
Attention :
La question essentielle est donc de savoir si la proportion est directe ou inverse. C'est de la réponse à cette question que de manière logique dépend la décision de multiplier ou de diviser. La méthode du passage par l'unité convient alors, aussi bien pour les grandeurs directement proportionnelles que si elles sont inversement proportionnelles.
N.B. Le passage par la valeur 1 n'est pas toujours indispensable. Si dans l'exemple ci-dessus la question avait été « Que coûtent 300 m de câble ? » on pourrait compter d'abord le prix de 100 m (4 x 25 m) puis multiplier ce résultat intermédiaire par 3 pour 3 x 100 mm.





