
Numération Binaire
La numération binaire est une numération en base 2.
En binaire il n'y a donc que deux chiffres 0 et 1.
Remarquez qu’en base 2, le chiffre 2 n’existe pas, tout comme le chiffre 10 n’existe pas en base 10.
Il s’agit d’une numération de position et suit en cela les mêmes principes que la numération décimale que nous connaissons bien. De droite à gauche nous avons donc les unités et ce que nous pourrions appeler les "deuzaines", les "quatraines", les huitaines, les seizaines, les "trente-deuzaines" etc. Et tant pis si ce n’est pas français !
Poids des bits
Prenons l'exemple du nombre binaire 10110 ?
Nous avons vu au chapitre intitulé "Numération de position" que :
Le poids d’un chiffre dépend de sa position et de la base
Poids = base position
Dans le cas du binaire cela devient :
Le poids d'un bit dépend de sa position et de la base
Poids = 2 position
Appliquons cette règle à notre exemple 10110(2)
| Exemple : 10110 en binaire → Poids de chaque bit = 2 position | |||||
|
Positions : |
4
|
3
|
2
|
1
|
0
|
|
Chiffres binaires |
1
|
0
|
1
|
1
|
0
|
|
Poids |
2 4 = 16
|
2 3 = 8
|
2 2 = 4
|
2 1 = 2
|
2 0 = 1
|
|
Valeur de chaque chiffre |
1 * 16
|
0 * 8
|
1 * 4
|
1 * 2
|
0 * 1
|
|
16
|
0
|
4
|
2
|
0
|
|
|
Valeur totale (comptée en décimal) |
16 + 4 + 2 = 22
|
||||
On a donc ici une seizaine , une quatraine et une deuzaine , soit 16 + 4 + 2 = 22
Un peu de vocabulaire : Bit, Byte, Octet, ... et autres Mots
Les codes binaires sont incontournables en informatique car l'information la plus élémentaire
y est le bit.
Ce mot « bit » est formé par la fusion des mots Binary digit
Ce qui en français se traduit par : Chiffre binaire
Un mot de 8 bits est appelé Octet (en français) et Byte (en anglais).
Les mots de 8, 16, 32 ou 64 bits sont courants. Ecrits en binaire, ils sont plus lisibles si laisse un espace entre les groupes de quatre bits comme ceci : 0100 0001
Un groupe de 4 bits est parfois appelé Quartet ou nibble mais ces termes sont peu utilisés.
Remarquez que l'on parle aussi de Mots binaires Word (en anglais) lorsque l'on veut spécifier la taille de ce mot. On dira de la sorte un mot de 32 bits ou un mot de 64 bits.
Zéros à gauche
Il est parfois intéressant de représenter les zéros non significatifs pour montrer la taille des codes transcrits. Il arrive que ces 0, à gauche des nombres, ne soient pas "non significatifs". En effet, les codes binaires ne représentent pas toujours des valeurs numériques. Ce sont parfois simplement des codes qui ne représentent ni des quantités ni des valeurs ordinales. Inutile donc de faire de l'arithmétique avec ces codes. Dans ce cas cela n'a aucun sens non plus de vouloir les convertir en décimal et ce serait une erreur d'omettre l'écriture de ces zéros à gauche du code.
![]()
Les amateurs de formulations mathématiques se plairont à souligner que les bits nécessaires pour écrire la valeur N proviennent de la série des coefficients du polynôme suivant :
N = b n-1 . 2 n-1 + ... + bi .2 i
+ ... + b2 . 2 2 + b1 . 2 + b 0
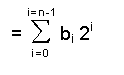
Les coefficients b n-1 ... b i ... b 2 , b 1 et b 0 valent chacun 0 ou 1.

