Numération de position
Ecriture des nombres
On a vu que les nombres peuvent être formés en utilisant plusieurs bases de numération : la base 10 (décimale), la base 2 (binaire), etc. Le choix de la base ne suffit pas à expliquer comment nous écrivons les nombres. On utilisera pour cela une notation appelée numération de position. Pour comprendre de quoi il s’agit nous allons commencer par montrer ce que serait l’écriture des nombres sans cette numération de position.
Les chiffres romains
Considérons le nombre 1975 . On sait que les romains employaient eux-aussi le système décimal, la base 10, mais ils écrivaient leurs nombres différemment.
Voici comment 1975 s'écrit en chiffres romains : MCMLXXV
Cette écriture, plus compliquée mais encore utilisée dans certaines circonstances, se prête mal aux calculs écrits. Essayez donc de faire par écrit MMX moins MCMLXXV !
Pour les romains, mille, cent, dix et un ne pouvaient que s'écrire avec des signes différents car, sans le principe de la numération de position, ils ne pouvaient imaginer attribuer à leur chiffres des valeurs qui fluctuent selon leur position dans le nombre.
Ajoutez à cela le fait qu'ils ne connaissaient pas non plus le chiffre zéro. Ils n'avaient vraiment pas la chance que nous avons maintenant d'être familiarisés depuis notre plus tendre enfance à ces notions qui étonnamment n'ont été connues en occident qu'à partir du XIIe siècle alors que le mathématicien arabe Al-Khwarizmi, utilisait déjà le chiffre zéro au VIIIe siècle et qu'il était connue en Inde et probablement en chine bien avant encore.
La numération de position combinée à l'utilisation du chiffre zéro nous permet de représenter les nombre de manière bien plus efficace et facilite grandement les opérations arithmétiques.
C'est à eux que je destine ce lien : http://irem.u-strasbg.fr/php/articles/37_Lefort.pdf
La numération de position
Revenons au nombre 1975 écrit en base 10 comme nous en avons l'habitude.
La valeur que l'on attribue à chaque chiffre dépend donc
- du chiffre en lui-même ( la valeur qu'il représente quand il est seul )
- mais aussi, de sa position
Dans 1975, le 5 vaut 5 unités = 5 x 1
le 7 représente des dizaines, il vaut 7 x 10
le 9 qui suit représente des centaines, il vaut 9 x 100
le 1 compte pour un millier = 1 x 1000
Nous formons donc les nombres à l'aide d'une notation où la position est très importante.
Le chiffre le plus à droite représente des unités. En décimal, les chiffres suivants représentent les dizaines, puis les centaines etc. Nous numéroterons les positions en allant de droite à gauche. Ainsi les unités auront toujours la même et première position, la position 0, quelle que soit la taille du nombre.
3 |
2 |
1 |
0 |
1 |
9 |
7 |
5 |
La règle qui permet de déterminer le poids d'un chiffre est la suivante :
Poids d'un chiffre = base position
La valeur d'un chiffre est donc le produit de sa valeur propre et de son poids.
Le poids d'un chiffre est une puissance de la base et l'exposant y est la position du chiffre
comptée de droite à gauche en commençant par les unités.
On peut aussi considérer que la position d'un chiffre dans un nombre entier est le nombre
de chiffres qu'il y a à sa droite
Ainsi en base 10 :
En position 0 se trouvent les unités. Leur poids est 100
En position 1 se trouvent les dizaines dont le poids est 101
En position 2 : les centaines dont le poids est 102
En position 3 : les milliers dont le poids est 103
...
En position n : les milliers dont le poids est 10n
Voici ce que cela donne pour le nombre 1975 en décimal ( Base 10 ) :
Le poids du chiffre 5 est 100 , sa valeur est 5 x 100 = 5 x 1 = 5
Le poids du chiffre 7 est 101 , sa valeur est 7 x 101 = 7 x 10 = 70
Le poids du chiffre 9 est 102 , sa valeur est 9 x 102 = 9 x 100 = 900
Le poids du chiffre 1 est 103 , sa valeur est 1 x 103 = 1 x 1000 = 1000
Positions |
3 |
2 |
1 |
0 |
|
Chiffres |
1 |
9 |
7 |
5 |
|
Base Position = Poids |
10 3 = 1000 |
10 2 = 100 |
10 1 = 10 |
10 0 = 1 |
|
Valeur de chaque chiffre |
1 * 1000 |
9 * 100 |
7 * 10 |
5 * 1 |
|
1000 |
900 |
70 |
5 |
||
Valeur totale |
1000 + 900 + 70 + 5 = 1975 |
||||
1975 = 1x 103 + 9x 102 + 7x 101 + 5x 100
D'une manière plus théorique, on peut dire que la valeur d'un nombre N représenté par n
chiffres en base B est la valeur numérique d'un polynôme du n-1 ième degré où B est la base
et dont les coefficients sont entiers et inférieurs à B
N = c n-1 B n-1 + ... + c i B i + ... + c 2 B 2 + c 1 B + c 0
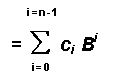
Exemple : En base 10, B=10 et les coefficients Cn-1, Cn-2, Ci, , C1, C0 ont tous une valeur inférieure à 10.
La suite de ces coefficients c n-1 c n-2 ...c 1 c 0 n'est autre que la suite des chiffres qui forment le nombre.
Mais, trêve de théories, revenons aux règles essentielles qu'implique ce qui a été vu jusqu'ici :
- Désormais, nous utilisons des numérations de position quelle que soit la base.
- Le chiffre le plus à droite représente toujours les unités
- Les positions des chiffres se comptent de droite à gauche
- La position du premier chiffre (celui de droite) est notée zéro
- Le second chiffre quand il vaut 1 représente exactement la valeur de la base quelle que soit cette base.
- Ajouter un zéro à droite d'un nombre revient à multiplier ce nombre par sa base.
Exercices
Un petit quizz pour ne plus se laisser piéger par la numération de position.
Exercices sur les nombres entiers en base 10
- On écrit un zéro à droite d'un nombre entier, de combien de fois sa valeur augmente-t-il ?
-
Combien y a-t-il de nombres entiers de deux, trois, quatre
chiffres
- Si on écrit les zéros non significatifs
- Si on n'écrit pas les zéros non significatifs
- Quel est le plus grand nombre exprimé par quatre chiffres significatifs ?
- Quel est le plus petit nombre exprimé par quatre chiffres significatifs.
- De combien le plus petit nombre de trois chiffres dépasse-t-il le plus grand nombre de deux chiffres ?
- Quel est le plus petit nombre exprimé par cinq chiffres significatifs différents ?
- Quel est le plus grand nombre exprimé par cinq chiffres significatifs différents ?
- Avec les chiffres 1, 2 et 3 former le maximum de nombres différents où chaque chiffre n'apparaît qu'une seule fois. Classer ces nombres par ordre croissant.
- Même question avec les chiffres 1, 2, 3 et 4
- Un livre possède 1000 pages, combien de fois a-t-on employé le caractère 0 pour numéroter ces pages ?
Quelques liens pour en savoir plus
