Conversion en une base quelconque :
Convertir un nombre entier dans une base quelconque
Rappel : Valeur de chaque chiffre
Nous avons vu au chapitre 4 comment convertir un nombre de base quelconque en base 10. Il suffit pour ce faire d’avoir compris le principe de la numération de position. Chaque chiffre à une valeur qui dépend 1° de sa valeur intrinsèque et 2° de sa position. On obtient la valeur d’un nombre en additionnant les valeurs des chiffres qui le composent.
Une autre manière d''’exprimer la même chose est de dire qu’en lisant un nombre de droite à gauche on rencontre les puissances successives de la base :
- unités, "deuzaines", "quatraines", huitaines, seizaines etc. pour le binaire ( base 2)
- unités, huitaines, "soixante-quatraines" etc. pour l’octal ( base 8)
- unités, dizaines, centaines, milliers, etc. pour le décimal (base 10)
- unités, seizaines, "deux-cent-cinquante-sixaines", etc. pour l’hexadécimal (base 16)
Voyons à présent comment coder dans une base B quelconque un nombre N dont on connaît la valeur décimale, c’est à dire son écriture en base 10. Il faut pour cela dénombrer les puissances successives de la base :
- le nombre d’unités, de deuzaines, de quatraines etc. pour convertir en binaire
- le nombre d’unités, de seizaines, etc. pour convertir en base 16
Il y a pour ce faire deux méthodes : de "gauche à droite" et de "droite à gauche".
Méthode intuitive : de gauche à droite
Quelle est la plus grande puissance p de la base B que l'on puisse retrouver dans N
et combien de fois y retrouve-t-on la valeur de Bp ?
Cela donne le premier chiffre à gauche, en position p.
Exemple : Soit à convertir 420(10) en base 16.
420(10) est supérieur à 162 ,
162 = 256 va une fois dans 420 ⇒ le chiffre le plus à gauche est 1
Reste à représenter 420 – 1 x 162 = 420 - 256 = 164 unités
On répète la même question tant que le reste est supérieur à la base.
164(10) est supérieur à 161,
161 va 10 fois dans 164 ⇒ chiffre suivant est A(16)
Reste 164 – 10 x 16 = 4 unités
Le nombre d'unités qui reste inférieur à B est le chiffre le plus à droite
autrement dit en position 0 si les positions sont numérotées de droite à gauche.
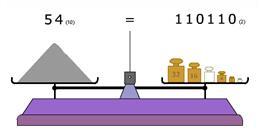
Retournez au besoin à l'exercice « Pesée d'un nombre binaire » pour vous habituer à évaluer les « poids des bits » qui composent un nombre en base 2.
Méthode systématique : de droite à gauche
Commençons par rechercher la valeur du premier chiffre à droite. Ce chiffre, les unités, est le reste de la division du nombre N à convertir par la base qu'ici nous appellons B. Ce chiffre en position 0 a un poids égal à la base exposant zéro = B0 = 1 = l'unité.
En divisant à nouveau le quotient de la division précédente par la base on obtient le chiffre de position 1 dont le poids est B1 = la base.
Des divisions répétées par la base donnent successivement les chiffres de poids B0, B1 B2 , B3 , B4 etc. ce qui nous permet d'écrire le nombre de droite à gauche.
Exemples :
1° Convertir 1830(10) en binaire ⇒ divisions successives par 2
| 1830 : 2 | = 915 | reste 0 | 0 × 20 = 0 unité |
| 915 : 2 | = 457 | reste 1 | 1 × 21 |
| 457 : 2 | = 228 | reste 1 | 1 × 22 |
| 228 : 2 | = 114 | reste 0 | 0 × 23 |
| 114 : 2 | = 57 | reste 0 | 0 × 24 |
| 57 : 2 | = 28 | reste 1 | 1 × 25 |
| 28 : 2 | = 14 | reste 0 | 0 × 26 |
| 14 : 2 | = 7 | reste 0 | 0 × 27 |
| 7 : 2 | = 3 | reste 1 | 1 × 28 |
| 3 : 2 | = 1 | reste 1 | 1 × 29 |
| 1 : 2 | = 0 | reste 1 | 1 × 210 |
| 0 | C'est fini, il ne reste plus rien à diviser | ||
Le résultat est : 111 0010 0110(2)
2° Convertir 1830(10) en hexadécimal ⇒ divisions successives par 16
| 1830 : 16 | = 114 | reste 6 | 6 × 160 = six unités |
| 114 : 16 | = 7 | reste 2 | 2 × 161 = 2 seizaines |
| 7 : 16 | = 0 | reste 7 | 7 × 16 2 = 7 × 256 |
| 0 | C'est fini, il ne reste plus rien à diviser | ||
Le résultat est 726(16) ce qui concorde bien avec la valeur trouvée en binaire 111 0010 0110(2)
Conclusions :
Ce procédé fonctionne pour toutes les bases mais en informatiques seuls nous concernent le binaire et l'hexadécimal, parfois mais plus rarement l'octal (base 8).
La conversion en binaire est la plus facile, le reste vaut 0 pour les nombres pairs et 1 pour les nombres impairs.
On a donc avantage à convertir d'abord en binaire. Le passage en hexadécimal comme nous l'avons vu au début du cours n'est plus alors qu'un jeu d'enfant.
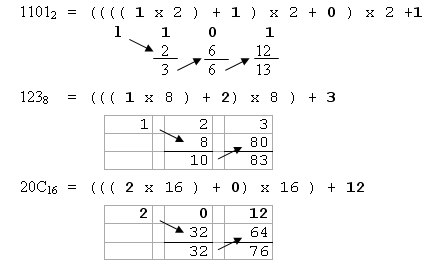
Autre méthode pour convertir d'une base B en base 10 « Méthode de Horner »
Nous avons vu comment calculer la valeur d'un nombre quelle que soit la base, utilisée pour le représenter. Nous additionnions les valeurs de chaque chiffre compte tenu de leurs positions dans le nombre.
La méthode qui suit donne le même résultat, ceux qui aiment les "recettes
de cuisines" la trouveront plus systématique.
Montrons comment cela marche pour le binaire
mais la méthode est valable quelle que soit la base.
Voici l'algorithme :
Exemples :
