Grandeurs et unités

Mesurer une grandeur, c'est la comparer à une autre de même nature prise comme unité. Ainsi, mesurer une longueur, c'est la comparer à celle du mètre, choisi comme référence. Mais nous pourrions tout aussi bien mesurer les longueurs en centimètres, en pouces, en yards etc. Et bien que le choix de l'unité soit arbitraire, les seules unités que nous utiliserons ici sont celles qui furent adoptées par le Système international d'unités de mesures (SI).

Unités fondamentales

Par soucis de standardisation le SI a opté pour 7 unités fondamentales correspondant aux 7 grandeurs physiques que voici :

• La longueur (L) que l'on mesure en mètres m
• La masse (M) comptée en kilogrammes kg
• Le temps (T) mesuré en secondes s
• L'intensité électrique (I) dont l'unité est l'Ampère A
• La température (Θ) mesurée en kelvins K
• La quantité de matière (N) comptée en moles mol
• L'intensité lumineuse (J) exprimée en candelas cd

Toutes les grandeurs de la physique peuvent être exprimées à partir de ces 7 unités fondamentales. Dans cette page seules les 4 premières unités fondamentales, celles du système mksA l’ancêtre du SI, suffiront pour définir les grandeurs les plus communes que l’on rencontre en physique.

Unités dérivées

Une unité dérivée est une combinaison d'unités fondamentales.
Ex.: la vitesse dont l'unité est le mètre par seconde \frac{m}{s}

Souvent les unités dérivées reçoivent un nouveau nom, un nom propre choisi pour rendre hommage aux scientifiques qui ont étudié cette grandeur de plus près ( Newton pour la force, Pascal pour la pression, etc.) Dans ce cas d'ailleurs, les symboles des unités s'écrivent avec une majuscule (N, Pa, Hz, J, W, ...) alors que les symboles des autres unités, celles dont les noms ne proviennent pas d'un nom propre s'écrivent en minuscules (m, kg, s, ...)

Quelques exemples :

• La pression se mesure en pascals   \textstyle 1 Pa = \displaystyle\frac{1 N}{1 m^2}
• La charge électrique est le produit de l'intensité du courant par le temps. Elle se compte en coulombs. 1 C = 1 A * 1 s
• La loi de Newton nous apprend qu'une force est le produit d'une masse par une accélération.
  Les forces se mesurent en newtons :  \textstyle 1 N = \displaystyle\frac{1 kg * 1 m }{1 s^2}

Grandeurs physiques, dimensions et unités

Les lois de la physique nous montrent que les différentes grandeurs mesurables, leurs dimensions et unités sont toutes reliées entre elles. Mais précisons d'abord le sens de chacun de ces mots.

Une grandeur physique est caractérisée par sa dimension et son unité. Une durée par exemple est une grandeur dont la dimension est le temps T pour lequel l’unité de mesure est la seconde.
La dimension dit de quelle nature est la grandeur sans préciser de quelle unité on se sert pour la mesurer.

Les 4 premières dimensions de base s'écrivent L pour les longueurs, M pour la masse, T pour le temps, I pour l’intensité. On se sert de crochets pour désigner les autres dimensions.
Ex.: La dimension d'une vitesse [v] est celle d'une distance L divisée par un temps T.

[v] = \tfrac{L}{T}   ou encore   [v] = L T^{-1}

Équations aux dimensions

L'égalité  [v] = L. T^-1 est appelée équation aux dimensions. Cette équation, où seules les unités entrent en compte, permet de vérifier l'homogénéité d'une formule en montrant que le résultat a bien la dimension de la grandeur recherchée.

Ex.: Vérifions l’homogénéité de la formule qui dit que la puissance d’une pompe = son débit volumétrique multiplié par la pression   \textstyle P = d \star p \quad \rightarrow \quad [P] = [d] \star [p]
Un débit = un volume / temps   \textstyle \rightarrow \quad [d] = L^3 T^{-1}
Une pression = force / surface   \textstyle \rightarrow \quad [p] = \frac { M L T^{-2}}{L^2} = M L^{-1} T^{-2}
\textstyle \Rightarrow \qquad [d] \star [p] = L^3 T^{-1} \star M L^{-1} T^{-2} = M L^2 T^{-3}
Reste à démontrer que les dimensions de base d’une puissance sont bien \small M L^2 T^{-3} pour pouvoir conclure que la formule proposée est homogène … Ce serait moins fastidieux si on ne s'obligeait pas à tout ramener aux unités de base !

Équation aux unités

Il est important de ne pas confondre dimensions et unités, mais ces deux notions sont étroitement liées. Et puisque ne nous servons uniquement des unités du SI, à une chaque dimension correspond une seule unité. La vérification de l’homogénéité d’une formule est plus rapide en raisonnant au niveau des unités.
Reprenons l'exemple précédent :     \textstyle P = p \star d
Pression p en \tfrac{N}{m^2}
Débit en \tfrac{m^3}{s}
\textstyle \Rightarrow \qquad \frac{N}{m^2} \star \frac{m^3}{s} = \frac{Nm}{s} = \frac{J}{s} = \textstyle W
On obtient des watts, c'est donc bien une puissance. La vérification est faite. Il suffit pour cela de connaître les unités de chaque grandeur et les relations entre les unités sans nécesairement revenir aux dimensions de base.

Représentation graphique

Le but de cette page est de montrer par un schéma comment sont reliées les grandeurs physiques et comment sont construites leurs unités du SI (Système international)

Conventions :

• Les grandeurs sont représentées par des points.
• Les relations entre ces grandeurs sont matérialisées par des vecteurs qui relient ces points/

Exemple : Soit un point d'origine représentant les nombres sans dimension. Des nombres tels que 0, 1, 2 , Pi, ...

A cette dimension purement arithmétique, ajoutons la notion de longueur (ou distance). Traçons pour ce faire un trait partant du point d'origine (les nombres sans dimension) et nous conduisant à un autre point qui représentera pour nous les longueurs (1cm, 25m, 340.000 km peu importe). Ce point nous l'appelons m car le mètre est l'unité choisie par le SI pour mesurer les longueurs.

Le trait qui relie le point "nombres sans dimension" au point "longueurs" est un vecteur. Chaque fois que nous voudrons multiplier une grandeur par une longueur (par des mètres) nous lui ajouterons ce même vecteur.

Si au point m on ajoute une nouvelle fois le vecteur "longueur", cela revient à multiplier des longueurs par les longueurs, autrement dit des mètres par des mètres et on obtient des m². Le point auquel aboutit la somme de ces vecteurs représente les surfaces. De la même manière, chaque fois que nous voudrons multiplier (ou diviser) une grandeur par des mètres nous ajouterons (ou retrancherons) le vecteur longueur.

En faisant de même avec un autre vecteur pour représenter les secondes, un autre vecteur encore pour les kilogrammes et au besoin un quatrième vecteurs pour les ampères nous obtiendrons presque la totalité des grandeurs physiques. Chacune représentée par un point distinct dans notre graphique.

Autre exemple pour les électriciens

Partons d’un point d’origine "sans dimension" il représente les nombres purs.

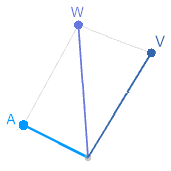
À cette grandeur purement arithmétique, ajoutons la notion de tension. On trace pour cela une flèche, nous dirons un vecteur, partant des nombres purs et représentant la relation "fois une tension". L’extrémité de ce vecteur représente une grandeur mesurable : la tension. Ce sera le point V car la tension se mesure en volts.

Soit A, le point représentant la grandeur physique intensité du courant. Sa position peut être quelconque, mais il ne peut être superposé au point V puisque ce sont deux grandeurs distinctes. Le vecteur qui va des nombres sans dimension au point A schématise la relation "fois une intensité" ou encore "fois des ampères".

Si on applique le vecteur "fois une intensité" à la grandeur tension, en traçant cette fois ce vecteur à partir du point V. Ou ce qui revient au même si on trace le vecteur V à partir du point A, on aboutit à un point qui est le produit de ces deux dimensions. Nous le noterons W car ce nouveau point représente la dimension puissance. (Puissance = Tension ∗ Intensité ↔ P = U ∗ I) Des volts fois des ampères donnent des watts (W).

En résumé : pour illustrer le produit des 2 grandeurs on fait la somme des vecteurs qui les représentent.

Voyons à présent comment, représenter la division d’une grandeur par une autre (encore que j’imagine que, dans votre grande sagacité, vous l’aurez deviné). On va illustrer la loi d’Ohm R = U / I

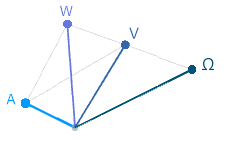
Pour diviser des volts (V) par des ampères (A) on va maintenant appliquer au point V l’inverse du vecteur A, c’est bien le même vecteur mais dirigé cette fois dans l’autre sens. On aboutit de la sorte au point Ω (Oméga est la lettre grecque, symbole de l’Ohm, l’unité de résistance électrique.

De la même façon, puisque toutes les grandeurs physiques sont reliées entre elles, il est possible de tracer un graphique schématisant de quelle manière les unités dérivées sont issues des unités fondamentales.

Les unités dites fondamentales ont été choisies par le SI (le Système international). A partir de vecteurs qui représentent ces quelques unités de départ, on va donc pouvoir élaborer une sorte de carte des unités qui montre comment elles dérivent des premières. L’aspect du schéma dépendra bien sûr des positions et des dimensions que vous donnez aux vecteurs initiaux. Une fois que ces premiers vecteurs ont été dessinés, tout le reste du graphique en dépend.

J'encourage les étudiants qui abordent ces matières à prendre leurs crayons et du papier pour essayer de faire eux-même leur propre carte des grandeurs physiques.

Un héritage qui ne pouvait être perdu

Le lien que voici vous montrera la carte telle que je l’avais dessinée dans les années 70. J’étais dans l’enseignement technique et on nous présentait les choses de la sorte à décloisonner les différents cours que nous avions : la mécanique, l’électrotechnique, la physique et même les mathématiques..

Maintenant que je suis à la retraite, je m’aperçois que nulle part sur Internet je ne retrouve cette façon de présenter le sujet. Je considère que cet enseignement dont j’ai bénéficié est un héritage qu’il serait dommage de perdre. C’est pour cette raison et pour m’occuper en ces temps de confinement que j’ai mis en musique (sur un air de javaScript) ce précieux apprentissage. Ce sera je l’espère pour certains un nouvel éclairage pour se familiariser aux grandeurs et aux unités qu’ils rencontrent en physique.

Toutes vos remarques seront les bienvenues. Je continuerai encore certainement à peaufiner cette page.