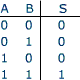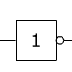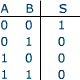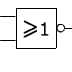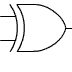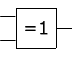Fonctions logiques de base
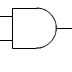
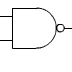
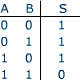
Porte AND
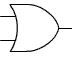
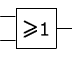
Porte OR
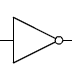
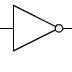
Porte NOT

Combinaisons de fonctions
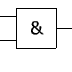
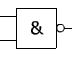
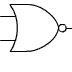
Porte NAND
Porte NOR
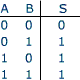
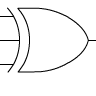
Porte XOR

Circuits fréquents :
Le comparateur
Le demi additionneur
Le plein aditionneur

Cliquez sur les entrées des portes
pour en tester le fonctionnement.

Les portes logiques

Nous avons jusqu'ici utilisé des boutons poussoirs et une lampe pour illustrer le fonctionnement des opérateurs logiques. En électronique digitale, les opérations logiques sont effectuées par des portes logiques. Ce sont des circuits qui combinent les signaux logiques présentés à leurs entrées sous forme de tensions. On aura par exemple 5V pour représenter l'état logique 1 et 0V pour représenter l'état 0.

Fonctions logiques de base

Porte AND

Table de vérité d'une porte ET à deux entrées

Porte OR

Table de vérité d'une porte OU à deux entrées

Porte NOT

Combinaisons des fonctions logiques de base

Porte NAND

Table de vérité d'une porte NAND à deux entrées

= NOT AND

Porte NOR

Table de vérité d'une porte NOR à duex entrées

= NOT NOR

Porte XOR

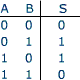
Table de vérité d'une porte XOR à deux entrées

La fonction "OU Exclusif" est en principe d'une fonction de deux variables :

S = A XOR B

La sortie est à 1 si une seule des deux entrées vaut 1.

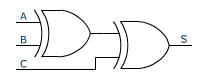
Porte XOR à plusieurs entrées

Pour calculer le résultat de S = A XOR B XOR C , il faut d'abord faire l'opération entre deux termes, puis refaire un ou exclusif entre le résultat obtenu et le troisième terme.

Ce qui se traduit par S = ( A XOR B) XOR C ou par S = A XOR ( B XOR C)

On constate que l'appellation "Ou exclusif" n'est tout à fait exacte que pour deux variables. Avec trois variables, le résultat vaut 1 si une d'entre elles ou toutes les trois valent 1.

Le résultat est en fin de compte un bit de parité. Il vaut 1 si le nombre d'entrées à 1 est impair.

Circuits logiques qui jouent un rôle important dans le hardware

Comparateur

Le comparateur est un circuit qui compare deux mots de n bits.
En sortie, un bit indique le résultat de la comparaison :
1 s'il y a égalité entre les deux codes présents à l'entrée, 0 si ces codes sont différents.

Le demi additionneur

Addition de 2 bits

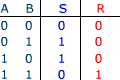
S = A xor B
est la somme

R = A and B
est le report

Le demi additionneur effectue la somme de deux bits. S est la somme et R le report. (carry)
Ce schéma n'est cependant pas suffisant pour réaliser la somme de nombres de plusieurs bits. Il faut alors tenir compte du report de l'addition des bits précédents.

Le plein aditionneur

Addition de 3 bits

Exemple : Calculons 1 + 3 . En binaire cela donne : 0001 + 0011

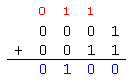L'addition des bits de droite est une addition de deux bits, elle peut être réalisée avec le demi additionneur. Pour les bits suivants par contre, il faut tenir compte d'un éventuel report.
Ainsi dès le deuxième bit de notre exemple (en comptant les bits de droite à gauche) il a fallu faire 2 additions ( 1 + 0 + 1 = 10 " on pose 0 et on reporte 1")

Table de vérité et équations et schéma du circuit plein additionneur

Cette table de vérité comporte 3 entrées : R n-1 (le report de l'addition précédente), A et B

Il lui faut deux sorties :

S = la somme de 3 bits (A + B + R n-1 )
R = le nouveau report

Addition de deux nombres de plusieurs bits

Exemple : Mise en cascade de 4 additionneurs pour l'addition de deux nombres de 4 bits

Numero(Chapitre);