Numération hexadécimale
Chiffres hexadécimaux
Il faut 16 chiffes pour écrire les nombres en base 16. Aux 10 chiffres du système décimal (0 à 9) ajoutons les 6 caractères A, B, C, D, E et F pour représenter ce que nous considèrerons ici comme étant les "chiffres" de 10 à 15.
Remarquez qu’en base 16, le chiffre 16 n’existe pas ; tout comme le chiffre 10 n’existe pas en décimal ni le chiffre 2 en binaire. Les principes de la numération de position sont applicables à toutes les bases et en particulier pour celle qui nous occupe ici, la base 16 :
- Le poids d’un chiffre dépend de sa position et de la base
- Poids = baseposition ici en hexadécimal le poids = 16 position
| Exemple : 1A2F hexadécimal → Poids de chaque chiffre = 16 position | |||||
|
Positions : |
3 | 2 | 1 | 0 | |
|
Chiffres binaires |
1 | A | 2 | F | |
|
Poids |
163 = 4096 | 162 = 256 | 161 = 16 | 160 = 1 | |
|
Valeur de chaque chiffre
|
1 × 4096
|
10 × 256
|
2 × 16
|
15 × 1
|
|
| 4096 | 2560 | 32 | 15 | ||
|
Valeur totale (comptée en décimal) |
4096 + 2560 + 32 + 15 = 6703
|
||||
On peut concevoir les nombres en base 16 comme une suite de coefficients d'un
polynôme dont chaque terme est fait à partir des puissances successives de 16
N = cn 16n + ... + ci 16i + ... + c2 162 + c1 16 + c0
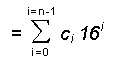
Pourquoi utiliser la base 16 ?
Les codes hexadécimaux sont bien pratiques en informatique. Ils représentent les codes binaires de manière compacte et nous évitent de devoir lire de longues enfilades de 0 et de 1 qui conviennent mieux aux ordinateurs qu’aux humains.
Un groupe de quatre bits permet de former 16 combinaisons différentes. On peut faire correspondre un chiffre hexadécimal à chacune de ces combinaisons de 4 bits. L’hexadécimal est en quelque sorte du binaire condensé.
Le code hexadécimal 1A2F est bien plus lisible que 0001 1010 0010 1111 en binaire
| Décimal | Binaire | Hexa |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Hexadécimal / Binaire - Mode d’emploi
Il est essentiel est de savoir compter jusqu’à 15 en binaire et en hexadécimal.
Exercez-vous à reproduire le tableau ci-dessous jusqu’à ce que vous sachiez compter sans aucune difficulté de 0 à 15 en binaire et en hexadécimal.
L'étape suivante de votre apprentissage sera de vous exercer à faire la correspondance entre les 16 codes binaires et les codes correspondants en hexadécimal.
Conversion Hexadécimal → Binaire
Remplacer chaque chiffre hexadécimal par le code de 4 bits correspondant.
Exemples :
7A6C (16) = 0111 1010 0110 1100 (2)
1234 (16) = 0001 0010 0011 0100 (2)
Conversion binaire → Hexadécimal
Grouper les bits par tranche de 4 en commençant à partir de la droite, puis chercher dans la table ci-dessus quel chiffre hexadécimal correspond à chaque quartet.
Exemple :
10100011011110 (2) = 0010 1000 1101 1110 = 28DE (16)
