
Nombres signés
Nous avons jusqu'à présent parlé de nombres entiers naturels. Ils ne peuvent par nature qu'être positifs ou nuls. Envisageons maintenant les nombres entiers relatifs ou autrement dit, munis d'un signe ‘+’ ou ‘-’
En décimal,
+1, +2, +3 etc. sont des nombres positifs. Ils sont supérieurs à 0 ( n >0 )
-1, -2, -3 etc. sont des nombres négatifs. Ils sont inférieurs à 0 ( n < 0 )
De même en binaire,
+1, +10, +11, +100, +101 etc. sont des nombres binaires positifs,
-1, -10, -11, -100, -101 etc. sont des nombres binaires négatifs.
Le problème est que les circuits électroniques digitaux ne peuvent enregistrer que des 0 ou des 1 mais pas de signes + ou -. Le seul moyen est alors de convenir que si un nombre est susceptible d'être négatif, on lui réserve un bit pour indiquer le signe. Reste à déterminer le bit qui dans un nombre binaire conviendrait le mieux pour symboliser le signe et quelle valeur de ce bit (0 ou 1) conviendrait le mieux pour représenter le signe "plus" ou le signe "moins".
Observons d’abord le fait que les nombres codés en machine ont une dimension fixe :
- Sur papier , les nombres ont des dimensions variables :
- L'addition de deux nombres de 2 chiffres donne un nombre de 2 ou 3 chiffres.
- La multiplication de deux nombres de 2 chiffres donne des nombres de 3 ou 4 chiffres.
- En machine par contre, les nombres ne sont pas extensibles. Ils ont des dimensions fixes. C'est exactement ce que nous avons avec certain compteurs.

Dans une voiture par exemple, le compteur kilométrique s'il ne possède que 6 chiffres ne pourra indiquer plus de 999.999 km .
De même, dans les ordinateurs les nombres (binaires) ont aussi des dimensions fixes de 1, 2, 4 ou 8 octets.
Revenons à l'exemple de la voiture et imaginez un compteur kilométrique qui compte les km en marche avant et qui les décompte en marche arrière. Que pourrait-on lire sur un compteur d'une voiture neuve (compteur initialement à 000.000) si elle parcourt 1 km en marche arrière ? Le compteur décompte 1 km et affiche donc ... 999.999 km ! Ce code correspond parfaitement à la valeur –1 puisqu'on obtient 0 si on lui ajoute à nouveau 1.
x + 1 = 0 ⇒ x = -1 ⇒ dans ce cas ci 999.999 équivaut à -1
On exploite cette caractéristique étrange qui est due au fait que ce nombre à une dimension finie ( 6 chiffres décimaux)
De même, quel serait le code d'un nombre de 8 bits pour représenter la valeur –1 ?
Le code 1111 1111(2) = FF(16) convient puisque, si on ajoute 1 à ce nombre, on obtient 00000000(2)
= 00(16), le bit de report déborde à gauche, il sort de l'espace qui est réservé au nombre et est donc ignoré.
Le bit le plus à gauche du mot binaire est celui qui va représenter le signe. Signe négatif si ce bit vaut 1, signe positif quand ce bit vaut 0.
| Nombre de 8 bits | |||
|---|---|---|---|
| Lu en
hexadécimal |
Lu en
binaire |
Lu en
décimal signé |
Lu en
décimal non signé |
| 7F | 0111 1111 | +127 | 127 |
| 7E | 0111 1110 | +126 | 126 |
| ... | ... | ... | ... |
| 10 | 0001 0000 | +16 | 16 |
| 0F | 0000 1111 | +15 | 15 |
| 0E | 0000 1110 | +14 | 14 |
| 0D | 0000 1101 | +13 | 13 |
| 0C | 0000 1100 | +12 | 12 |
| 0B | 0000 1011 | +11 | 11 |
| 0A | 0000 1010 | +10 | 10 |
| 09 | 0000 1001 | +9 | 9 |
| 08 | 0000 1000 | +8 | 8 |
| ... | ... | ... | ... |
| 02 | 0000 0010 | +2 | 2 |
| 01 | 0000 0001 | +1 | 1 |
| 00 | 0000 0000 | +0 | 0 |
| FF | 1111 1111 | -1 | 255 |
| FE | 1111 1110 | -2 | 254 |
| FD | 1111 1101 | -3 | 253 |
| FC | 1111 1100 | -4 | 252 |
| FB | 1111 1011 | -5 | 251 |
| FA | 1111 1010 | -6 | 250 |
| F9 | 1111 1001 | -7 | 249 |
| ... | ... | ... | ... |
| 86 | 1000 1001 | -122 | 134 |
| 85 | 1000 0101 | -123 | 133 |
| 84 | 1000 0100 | -124 | 132 |
| 83 | 1000 0011 | -125 | 131 |
| 82 | 1000 0010 | -126 | 130 |
| 81 | 1000 0001 | -127 | 129 |
| 80 | 1000 0000 | -128 | 128 |
Si on admet que le nombre peut représenter des valeurs négatives, on parle de nombres "signés".
Comme pour les nombres "non signés", on peut représenter 28 = 256 codes avec 8 bits
mais ici le bit de gauche est le signe
1 = signe moins
0 = signe plus
Il y a donc moyen de représenter
- 128 codes avec le bit de signe à 1
ce sont 128 nombres négatifs
( de –1 à – 128) - 128 codes avec le bit de signe à 0
le nombre 0 et 127 nombres positifs
( de 1 à +127)
Comment calculer les codes des nombres négatifs ?
Le calcul se fait en deux étapes :
1° Calcul du complément à 1 = Remplacer tous les 0 par des 1 et tous les 1 par des 0.
2° Calcul du complément à 2 = Ajouter 1 au complément à 1
Exemple : comment écrire – 4 en binaire ou en hexadécimal ?
+ 4 = 0000 0100(2)
Le complément à 1 de ce code est 1111 1011(2)
Ajoutons 1 à ce code pour obtenir son complément à 2
1111 1011(2) + 1 = 1111 1100(2) = FC(16) = - 4(décimal signé)
Cas particuliers :
- Le complément à 2 de 0 est encore 0
- Le complément à 2 de 80H est aussi 80H ! Les nombres négatifs et positifs ne sont pas répartis symétriquement.
Avec un byte la valeur minimum est –128 contre +127 pour la valeur positive.
NB. Le complément à 1 est aussi appelé " complément logique " ou " complément restreint "
De même, certains désignent le complément à 2 par l'expression " complément arithmétique ".
Analogie en décimal
Puisque deux chiffres suffisent pour écrire 25, 17 et 08 nous limitons la taille de ces nombres à 2 caractères. La question devient : Quel nombre faut-il ajouter à 25 pour que la réponse se terminer par les chiffres 08 ? Ce nombre est 83. En effet 25 + 83 = 1 08 mais on ignore le 1 à gauche puisque nous avons décidé de donner une taille fixe de deux chiffres pour les nombres de cet exemple. 83 est donc dans ce cas le complément arithmétique de 17. Comment trouver ce complément arithmétique en base 10 ? La méthode ressemble fort au calcul du complément à 1 comme en binaire suivi de l'addition d'une unité. Ici, en décimal, le complément restreint sera un complément à 9. Complément à 9 : 99 -17 = 82 Complément arithmétique : 82 +1 = 83 99 – 17 + 1 = 100 – 17 = 83 |
La valeur du bit de signe
Le bit de signe est le bit le plus significatif du code ( MSB Most Significant Bit ), celui qui est le plus à gauche. Dans le cas d'un nombre de n bits numérotés de 0 à n-1, c'est le bit n-1. Bien souvent on se contente de constater que ce bit est à 1 pour en conclure que le nombre considéré est négatif. La valeur absolue de ce nombre est alors déterminée en calculant le complément arithmétique de son code.
Une autre manière d'envisager la chose serait de considérer que le bit n-1 a, contrairement aux autres bits, une valeur négative : - 2n-1
Exemple :
Si un byte est considéré comme un code signé, le bit 7 quand il est à 1 vaut -128.
Si le byte est considéré comme non signé, le poids du bit 7 est simplement 27 = 128.
Ainsi -123 = -128 + 5 = 80H + 5 = 85H
Plus généralement :
• Pour les nombres non signés, nous calculions la valeur du nombre comme suit :
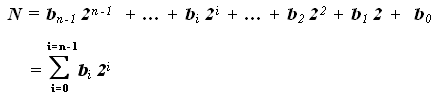
• Dans le cas des nombres signés, la valeur sera
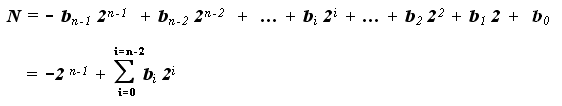
Extension de la taille d'un nombre signé
Pour étendre la taille d'un nombre non signé, on ajoute des 0 à sa gauche.
Pour étendre la taille d'un nombre signé, on ajoute sur la gauche des bits identiques au bit de signe.
Exemples :
-4 code sur un octet = FC(16) sur deux octets ce code devient FFFC(16)
FC(16) = 1111 1100(2) ≡ FFFC(16) = 1111 1111 1111 1100(2)
de même
+4 en un octet = 04(16) sur deux octets = 0004(16)
04(16) = 0000 0100(2) ≡ 0004(16) 0000 0000 0000 0100(2)
Exercices
1°
2° Autres questions :
- Déterminez les valeurs des compléments logiques et arithmétiques des codes binaires suivants :
Complément à 1 Complément à 2 1100 1001 0000 1111 0111 0011 0001 0000 - Calculer les compléments à 1 et à 2 pour les nombres suivants exprimés sous forme hexadécimale.
Faites le calcul en binaire puis notez la réponse en hexa.
AA(16)
FF(16)
1248(16)
- Que vaut le code C0(16)
• s'il s'agit d'un nombre non signé ?
• s'il s'agit d'un nombre signé ?
- Les codes suivants ont une taille de 16 bits, ils sont signés et donnés en hexadécimal. Calculez leurs valeurs et donnez la réponse en décimal.
FFFF
8000
7FFF
00FF
- Quelles sont les valeurs minimum et maximum que peut prendre un nombre entier signé codé sur 4 octets ?
- Comment écrire -512 en binaire ? Combien faut-il de bytes au minimum pour encoder cette valeur ?
- Quel est le plus petit nombre entier négatif qui puisse être traité dans les registres d'un Pentium 64 bits ?
- La valeur -192 peut-elle être codée sur un byte ? justifiez votre réponse.
- Comment écrire -150 en binaire et en hexadécimal ?
- Que vaut 8001(16) selon que ce code de 2 octets est signé ou non signé ?