Combinaisons de fonctions logiques

Combinaisons des 3 fonctions de base

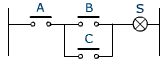
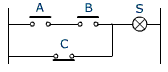
Les trois fonctions de base AND, OR et NOT se combinent de multiples façons. Ces combinaisons peuvent facilement être illustrées par des montages de contacts électriques.

Correspondance entre schémas et équations logiques

A chaque schéma imaginable correspond une équation. La correspondance entre un schéma et une fonction logique est systématique :
- Des montages en parallèle correspondent à la fonction OU
- Des montages en série correspondent à la fonction ET
- Un contact normalement fermé représente la fonction NON

Exemples :

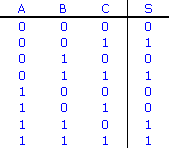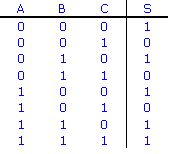
Tables de vérité

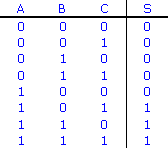
Pour tracer la table de vérité, que ce soit à partir d'un shéma ou d'une équation, il faut commencer par dénombrer les variables. Les exemples ci-dessus comportent chacun 3 variables (A, B et C).
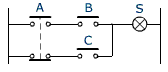
Il faut remarquer qu'une même variable peut intervenir plusieur fois dans une équation ou sur plusieurs contacts dans le schéma. C'est le cas de la variable A dans le troisième exemple.
On trace ensuite une table avec toutes les combinaisons possibles des n variables. Cela donne 2ⁿ combinaisons. 8 = 2³ dans nos exemples. Le plus facile est de noter toutes ces combinaisons en considérant qu'elles forment des nombres écrits en binaire et des les aligner une à une comme si l'on comptait en base 2. On est alors certain en faisant de la sorte de n'avoir oublier aucun cas.

Reste maintenant de déduire les valeurs à indiquer dans la colonne de droite.
Elles résultent du fonctionnement du schéma de contacts ou du calcul de ce que donne l'équation logique.

• Déduction à partir du schéma de contacts :
  On considère qu'un contact est actionné si la variable correspondante vaut 1. Le contact est dans sa position de repos (comme représenté sur le schéma) lorsque la variable correspondante vaut 0. Attention à ne pas confondre le fait qu'un contact soit actionné et le fait qu'il soit fermé. Un contact normalement ouvert laisse passé le courant quand il est actionné mais un contact normalement fermé laisse passer le courant quand il n'est pas actionné.
• Calcul à partir de l'équation logique :
  On substitue les variables par les valeurs qui leurs sont attribuées aux différentes ligne de la table de vérité.