Logique booléenne

Introduction

La logique, si l'on considère l'histoire des sciences, est une discipline très ancienne dont les traces les plus éloignées remontent aux philosophes Grecs. Logos en grec se traduit par parole et/ou raison. Aristote, parait-il, s'amusait à voir comment étaient construits les faux raisonnements ... Mais, ce n'est pas de cette logique là que nous traiterons ici.

La logique qui va nous occuper dans les pages suivantes concerne l'étude de fonctions logiques élémentaires qui traitent des variables binaires par des méthodes aussi systématiques que les mathématiques. Le but est ici de comprendre et démystifier autant que se peut la manière dont les ordinateurs effectuent les opérations logiques de base puis d'entrevoir comment ces fonctions peuvent être combinées pour obtenir des résultats de plus en plus complexes comme par exemple les opérations arithmétiques.

Variables logiques

Dans les systèmes digitaux (systèmes informatiques et autres automatismes numériques) toutes les données sont traitées et enregistrées à partir d'éléments d'informations binaires.

Ces informations binaires à la manière des contacts électriques n'ont que deux états possibles : un contact électrique est ouvert ou fermé, de même le bit est une information élémentaire qui ne peut prendre que deux valeurs 0 et 1.

Dans la suite de ce cours les variables logiques sont représentées par des lettres. Les valeurs de ces variables sont à priori indéterminées, elles sont « variables ». Ainsi, si l'on écrit l'équation logique « S = A » cela signifie que la variable logique S a exactement la même valeur que la variable A mais rien ne précise quelle est la valeur de A ( 0 ou 1 ?) On dira que A est une variable binaire puisqu'elle ne peut prendre à un instant donné qu'une des deux valeurs 0 ou 1.

NB. Un parallèle peut être fait avec les variables algébriques comme par exemple dans la fonction algébrique « y = 2x + 5 » Elle nous indique comment calculer y pour chaque valeur de x mais la valeur de x n'est pas figée. C'est ici une variable algébrique.

Les opérations logiques sont en informatique aussi courantes si pas plus que les opérations arithmétiques. La logique combinatoire tout comme l'arithmétique repose sur quelques opérations élémentaires.

• En arithmétique, ces opérations sont l'addition, la soustraction, la multiplication et la division ( +, -, *, / ). Il est possible à partir de là d'imaginer toutes les autres opérations telles que les exposants, les racines, les logarithmes etc.
• En logique, les opérations fondamentales sont le ET, le OU et le NON.
  Nous utiliserons des signes particuliers pour représenter ces trois opérations fondamentales lors d'écriture d'équations logiques. C'est George Boole, un mathématicien britannique, qui le premier eu l'idée de reprendre des notations algébriques pour créer les bases de ce qui sera la logique informatique. Nous ferons donc de la logique booléenne et aussi de l'algèbre booléenne en écrivant des équations logiques pour exprimer les relations entre les variables logiques appellées aussi variables booléennes.

Cette logique a trouvé après George Boole ses premières applications dans les circuits électriques. C'est Claude Shannon , un autre père fondateur des théories à la base de l'informatique, qui entreprit de mettre en équation les circuits électriques où des relais électriques considérés comme des variables logiques en agissent sur des contacts ouverts (0) ou fermé (1).

Fonctions logiques de base

La manière la plus simple de comprendre les fonctions logiques est de se les représenter par des schémas électriques qui comportent un ou plusieurs contactss et une lampe. Cette lampe s'allume "à condition" que les contacts électriques y laissent passer le courant. C'est dans l'expression de cette condition que va intervenir la logique.

Une table de vérité a pour le rôle de montrer la correspondance entre la sortie et toutes les combinaisons de valeurs que peuvent prendre la ou les entrées.

Le contenu de la table de vérité s'obtient en imaginant toute les configurations possibles pour le contact A (0 = contact relâché, 1 = bouton pressé). A chacun des états du contact A on vérifie d'après le schéma électrique ou d'après l'équation logique si la lampe est éteinte (0) ou allumée (1).

---

Plaçons maintenant deux contacts dans le circuit. La condition nécessaire pour allumer la lampe dépend de la manière dont les contacts sont connectés. Suivant les cas, la condition pour allumer la lampe fait appel aux opérateurs logiques ET ou OU.

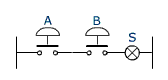
La fonction ET

La lampe s'allume si on active simultanément les contacts A et B

(S = 1)  si  (A = 1)  ET  (B = 1)

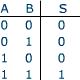
L'opérateur ET est représenté dans l'équation logique par un point. Ce signe convient parfaitement puisque la fonction ET donne le même résultat qu'une multiplication.

Le contenu de la table de vérité s'obtient en imaginant toute les configurations possibles pour le contact A (0 = contact relâché, 1 = bouton pressé). A chacun des états du contact A on vérifie d'après le schéma électrique ou d'après l'équation logique si la lampe est éteinte (0) ou allumée (1).

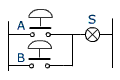
La fonction OU

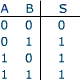
L'opérateur OU est représenté dans l'équation logique par un signe plus surmonté d'un point. Observons les trois premières ligne de la table de vérité, le résultat de l'opération OU y est semblable au résultat d'une addition. Le résultat de 1 ou 1 diffère cependant de 1+1. Nous mettons un point au-dessus du signe '+' pour indiquer que l'opération n'est pas analogue à une addition.

La fonction NON

Les contacts que nous avons utilisés jusqu'ici, sont des contacts "normalement ouverts". Quand le bouton poussoir est relâché ( quand A = 0) le courant ne passe pas.
Nous utilisons maintenant un contact "normalement fermé" pour illustrer la fonction NON. Au repos, le courant passe mais il se coupe quand le contact est activé ( quand A = 1).