Addition et soustraction de deux octets

Rappelons qu'un octet est un code de 8 bits.
On peut avec 8 bits représenter 2⁸ soit 256 combinaisons différentes.
Ces combinaisons varient 0000 0000 à 1111 1111  si on les écrit en binaire ou de 00 à FF si on les écrit en hexadécimal.

Le traitement automatique de l'information (de son codage) n'a d'intérêt que si les codes produits par ce traitement ont bien à leur tour des significations correctes. La question essentielle est donc de savoir quelles informations peuvent valablement être représentées par un codage déterminé.

Prenons l'exemple d'un octet.
Quelles sont les valeurs que peuvent représenter les diverses combinaisons possibles avec 8 bits ? La réponse dépend de la convention adoptée par celui qui utilise ces codes :

• Si pour nous, ces codes représentent des nombres non-signés, les 256 valeurs qui peuvent être représentées par un octet vont de 0 à 256 ( 00₁₆ à FF₁₆)
• Si par contre nous considérons ces codes comme représentant des nombres signés, les 256 valeurs possibles vont de -128 à +127 (80₁₆ à 7F₁₆)

Les opérations arithmétiques faites à partir de ces codes donnent des résultats corrects pour autant que les codes produits ne sortent pas des limites qui dépendent du codage choisi : la taille du nombre 8, 16, 32 ou 64 bits et le fait que ces nombres soient considérés comme signés ou non. En dehors de ces limites les codes produits ne correspondent plus à des valeurs correctes.

Exemple :

Imaginons le calcul donné ici en hexadécimal :   C0 + 2C

En binaire, cela s'écrirait :    1100 0000   +   0010 1100

Le résultat sera EC en base 16   ou ce qui revient au même   1110 1100   en binaire

Voyons maintenant si les codes produits correspondent à des réponses valables.

1. Si ces codes représentent des nombres non signés :
   Leurs valeurs sont donc comprises entre 0 et 255

   C0₁₆ ou 1100 0000₂   représentent  la valeur 192 écrite ici en décimal

   2C₁₆ ou 0010 1100₂   représentent  la valeur 44 en décimal

   Le résultat EC₁₆ représente 236.   Cela correspond bien à la valeur 192 + 44

   Le résultat est correct car nous sommes restés dans les limites des nombres non signés.
   Nous ne sommes pas passés sous la valeur zéro. Il est d'ailleurs impossible d'écrire des nombres négatifs avec des nombres non signés !

   Nous n'avons pas non plus dépassé la valeur maximum de 255.

2. Si ces codes représentent des nombres signés :

   Leurs valeurs sont donc comprises entre -128 et + 127

   C0₁₆  ou   1100 0000₂ représentent la valeur négative -64

   2C₁₆   ou   0010 1100₂ représentent la valeur positive +44

   Le résultat ED₁₆ représente -20 cela correspond bien à la valeur de (-64) + (+44)

   Le résultat est correct car nous sommes restés dans les limites des nombres non signés
   Nous ne sommes pas passés sous la valeur de -128

   Nous n'avons pas non plus dépassé la valeur maximum de + 127 

Voyons comment de tels calculs peuvent être réalisés de manière automatique par un dispositif qui pourtant ignore la signification c'est-à-dire la valeur des codes qu'il traite.

Le dispositif en question sera une calculatrice hexadécimale réalisée en papier. Elle est constituée de deux disques concentriques représentés ci-dessous et disponnibles dans les pages 4 et 5 du document pdf  associé à cette page.
Ces disques sont gradués avec les 256 codes allant de 00 à FF.

Le disque intérieur sera découpé et fixé avec une punaise au centre du disque extérieur.

 

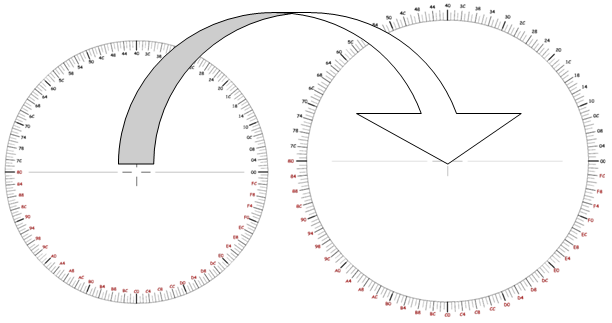
L'opération précédente C0 + 2C peut maintenant être réalisée en faisant pivoter le disque intérieur de sorte à placer l'origine de son origine la graduation (00) en face de l'inscription C0 sur le disque extérieur. Cherchons maintenant la valeur 2D à additionner sur le disque intérieur. La somme EC lui fait face sur le disque externe.

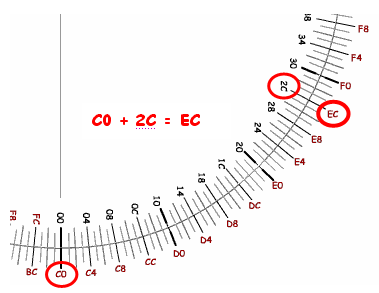
Ce calcul C0 + 2C = EC donne un résultat correct quelle que soit la convention utilisée (nombres non-signés ou au contraire signés) car ni dans un cas ni dans l'autre nous n'avons franchi les valeurs limites que peuvent représenter ces codes de 8 bits

Nombres non signés : 192 + 44 = 236   et     0 < 236 < 255

Nombres signés :         -64 + 44 = 20   et     -128 < 20 < +127

 

Il n’en sera pas de même si l’on dépasse l’une des limites liées à la convention utilisée (nombres signés ou non signés)

 

Ainsi si on voulait représenter deux nombres 120 et 40 par un code signé d'un seul octet .

Ces deux nombres peuvent sans problèmes être représentés par un octet signé puisqu'ils sont compris entre les valeurs limites -128 et + 127.        +120 = 78₁₆    et     +40 = 28₁₆

Par contre, leur somme 120 + 40  vaudra 160 ce qui est une valeur supérieure à  +127

La valeur 160 ne peut donc pas être représentée de manière valable par un code signé d'un seul octet !   Ce dépassement sera signalée par un flag particulier du processeur : l'Overflow

On aurait donc du utiliser des nombres d’au moins 2 octets pour faire des calculs valides avec de telles valeurs.
0078₁₆ + 0028₁₆ = 00A0₁₆    = 160₁₀

 

Imaginons maintenant que l'on veuille additionner 250  + 16 avec des nombres non signés d'un seul octet.

Bien que, comme dans le cas précédent, les deux nombres de départ peuvent sans problème être représentés par un seul octet  ( 250 = FA₁₆) et (16 = 10₁₆) 

Le résultat que donnerait notre calculatrice en papier ou n’importe quel microprocesseur sera  0A₁₆ = 10 en décimal.
Pourtant     250 + 16 ne vaut pas 10 !
L'erreur est due au fait que le résultat qu'on aurait dû obtenir 266 dépasse la valeur limite (256) possible avec un nombre non signé d'un seul octet.

Les microprocesseurs indiqueront le dépassement de cette limite par un flag de Carry (report)

Il aurait fallu au moins 2 octets pour coder ces nombres : 00FA + 0010 = 010A