Historique

Les origines de l'informatique

Si l'informatique en tant que telle n'existe que depuis quelques dizaines d'années, ses origines sont issues de nombreux domaines et remontent pour certaines à très longtemps. Citons par exemple les abaques et les bouliers compteurs. Ce sont les premiers instruments d'aide aux calculs. On verra de même que l'histoire de la numération n'est pas sans intérêt pour nous aider à comprendre la numération de position et plus particulièrement les codes binaires.

Machines à calculer

Bouliers et abaques

Le boulier compteur originaire d'Asie où il compte encore des adeptes, serait la première "machine à calculer". Il n'est à vrai dire qu'un appareil permettant d'enregistrer les calculs. Bien que très élémentaire cet instrument possède déjà quelques caractéristiques instructives. Nous nous en servons pour illustrer ce qu'est la numération de position : le boulier comporte plusieurs tiges, chacune correspond à la position d'un chiffre (unités, dizaines, centaines, milliers, etc.) Sur ces tiges sont enfilées des boules dont la position forme un code allant de 0 à 9 ou de 0 à 10 selon les modèles de boulier. Les bouliers facilitent le calcul en "affichant" et donc en "mémorisant" le résultat de la dernière opération.

Les abaques romains étaient eux aussi des instruments d'aide à la représentation, à la mémorisation et à la manipulation des nombres. Les boules du boulier sont ici remplacées par des cailloux (calculi en latin) placés dans des encoches parallèles représentant chacune les multiples de 1, 10, 100, 1000 etc.

Pour nous qui sommes habitués aux chiffres arabes, il est étrange de constater qu'il a fallu si longtemps à nos ancêtres pour adopter une écriture des nombres basée sur la numération de position comme le faisaient pourtant les bouliers et les abaques. Les romains par exemple étaient obligés de changer de signes pour écrire le chiffre 1 selon qu'il représente une unité (I) une dizaine (X) une centaine (C) ou un millier (M). Imaginez dans ces conditions comme il devait être difficile de faire des calculs écrits.

La numération de position (ainsi que le chiffre zéro) aurait été imaginée en Inde au IV^ème ou au V^ème siècle ; elle fut adoptée par le mathématicien arabe Al-khawarizmi vers l'an 820 et s'imposa en occident après les croisades XII^ème ou XIII^ème siècle.

Règle à calcul

La règle à calcul fut inventée en 1620. Elle permet de faire des calculs approchés : multiplications, divisions, racines carrées, logarithmes etc. et a été utilisée jusqu'au milieu des années 70 (les ingénieurs de la Nasa qui ont envoyé Apollo sur la lune l'utilisaient encore) Les principes de cette règle à calculer remontent au mathématicien écossais John NAPIER (1550-1617) plus connu sous le nom de Néper.

Néper avait imaginé qu'il devrait être possible de transformer une opération de multiplication en simple addition et il inventa pour ce faire les logarithmes.
Le logarithme en base b d'un nombre N est l'exposant qu'il faut donner à la base b pour obtenir ce nombre N.
Toutes les bases de logarithme sont imaginables et celle préconisée par Neper fut le nombre e = 2,71828. Ce nombre a des propriétés particulières et est connu comme la base des logarithmes Népériens notés "ln" sur les calculatrices scientifiques. La base 10 est aussi couramment utilisée (touche Log de nos calculatrices scientifiques) Cette base 10 est aussi plus commode pour démontrer l'intérêt des logarithmes.
Exemples :
Log₁₀ 1000 = 3 , ce qui se lit : "logarithme en base 10 de 1000 = 3".
De même Log₁₀ 100 = 2 car 10² = 100 et Log₁₀ 0,001 = -3 car 10^-3 = 0,001
Ces exemples simples vous permettront de vérifier les propriétés suivantes : log (A*B) = log A + log B     et     log (A/B) = log A - log B
On obtient ce que Néper avait recherché : une méthode pour transformer les multiplications en simples additions ou des divisions en simples soustractions.

Machines à calculer mécaniques

La première machine à calculer mécanique date de 1623 et était appelée "horloge à calcul" par son inventeur, l'astronome allemand : Wihelm SCHICKARD (1592- 1635)

Blaise PASCAL (1623-1662), philosophe et mathématicien français réalisa à son tour, alors qu'il n'avait encore que 19 ans, une machine à calculer mécanique : la Pascaline. Elle était constituée d'une série de roues dentées, numérotées de 0 à 9 et agencées de manière telle que chaque tour complet d'une roue fasse avancer la suivante d'une position. Cette machine construite en 1642 ne pouvait faire que des additions et des soustractions.

En 1673, LEIBNIZ (1646 - 1716) mathématicien allemand et (lui aussi) philosophe, perfectionna la Pascaline pour en faire une machine capable d'effectuer des multiplications, des divisions et des racines carrées par additions ou soustractions successives.

Premiers automatismes

Les premiers automatismes capables d'exécuter des séquences d'opérations dont le déroulement était préenregistré furent d'abord sans lien avec le calcul. Dès le XIV^ème siècle, de grandes horloges dont certaines ornent encore nos clochers ou nos beffrois sonnaient les heures selon des séquences complexes suivant qu'il s'agissait des heures, de demi-heures etc.

Les automates très en vogue au XVIII^ème siècle imitaient les êtres vivants. Il y eu même un joueur d'échec artificiel qui aurait battu Napoléon mais c'était une supercherie, un nain caché sous la table actionnait les mécanismes.

En 1725, Basile BOUCHON eu l'idée d'automatiser une machine à tisser la soie en enregistrant les séquences d'opérations sur des bandes perforées. C'est probablement la première fois que l'on enregistre une séquence d'opérations sur un support amovible qui sera lu ensuite par une machine automatique pour en recevoir les instructions.

Le métier à tisser automatique le plus célèbre fut celui de Joseph-Marie JACQUARD (1752-1834) mis au point en 1805. Les motifs du tissage étaient programmés à l'aide de cartes perforées. Les fils de chaîne qui sont levés ou baissés entre chaque passage de la navette sont suspendus à des crochets qui peuvent ou non se lever selon qu'ils se trouvent ou non sous des trous dans la carte perforée. Chaque passage de la navette correspond à ce que les tisserands appellent une trame. A chaque trame correspondait une nouvelle carte perforée et le motif tissé était défini par une succession de cartes perforées que l'on appelait un "programme". C'est ce terme que l'on utilise actuellement pour désigner une suite d'instructions en informatique.

Babbage

L'ingénieur anglais Charles BABBAGE (1792-1871) fut le concepteur de deux machines qui, bien qu'elles ne purent être réalisées à son époque pour des raisons techniques et financières, ont le mérite d'être à l'origine de concepts que l'on retrouve encore dans nos ordinateurs.

La première de ces machines fut la "difference engine". Il faut savoir qu'à cette époque, les calculs complexes (astronomie, navigation, artillerie etc.) se faisaient à l'aide de tables numériques : tables trigonométriques et tables de logarithmes. Ces tables comportaient trop souvent des fautes et c'est entre autre pour cette raison qu'en 1821, Charles Babbage entrepris de concevoir une machine capable de réaliser les nombreux calculs répétitifs nécessaires à la confection de ces tables selon la méthode dite "des différences finies", d'où le nom de cet engin !

Le projet était très (trop) ambitieux, cette machine après avoir calculer les valeurs à inscrire dans les tables devait estamper les plaques de plomb qui auraient servi à l'impression des pages de résultats. Il aurait fallu 25000 pièces pour construire cette machine, 10 ans plus tard, 12000 pièces seulement avaient été fabriquées et le projet fut abandonné en 1832.

Constatant que de toutes façons la difference engine n'aurait été capable de ne faire que les calculs pour lesquels a été conçue, Babbage entrepris la réalisation d'une autre machine, universelle celle-là, l'"Analytical engine" capable d'exécuter n'importe quelle séquence d'opérations mathématiques au moyen d'instructions enregistrées sur des cartes perforées comme dans le métier Jacquard.

La "machine analytique", entièrement mécanique avait déjà une architecture très proche de celle des ordinateurs actuels. On y retrouve plusieurs concepts de base tels que :

• une unité d'entrée pour recevoir les cartes perforées lui communiquant à la fois les instructions et les données.
• une unité de traitement que Babbage appelait the mill (le moulin) et qui préfigurait les unités arithmétiques et logiques de nos processeurs actuels.
• une unité de commande (control unit) qui supervise automatiquement la succession interne des opérations (chercher les données en mémoire, les placer dans le moulin, commander telle ou telle opération arithmétique, transférer les résultats etc.) Cette unité de commande comportait aussi un repeating aparatus destiné à reprendre en boucle autant de fois que nécessaire une série d'instructions.
  C'est la séparation de l'unité de commande de l'unité d'exécution qui donne la possibilité à la machine de faire n'importe quel algorithme contrairement aux machines précédentes construites pour ne faire que des séquences d'opérations déterminées.
• une unité que Babbage appelait le magasin (store) où sont rangées les données à traiter, les résultats intermédiaires et les résultats finaux destinéés à être sortis sur des cartes perforées. Cette unité regroupe donc ce que l'on appelle aujourd'hui la mémoire et l'unité de sortie mais Babbage n'avait pas fait de distinction entre ces deux fonctions pas plus qu'il ne faisait analogie entre cet espace de rangement de données et mémoire humaine.

Ada LOVELACE (1815-1852) fut une collaboratrice de Charles Babbage pour la conception de sa machine analytique. Elle définit le principe des itérations et définit les principes de la programmation de la machine de Babbage.

Elle fit la description complète de la machine de Babbage et rédigea à ce propos certains articles en français. On peut y lire "la machine analytique tissera des motifs algébriques comme les métiers de Jacquard tissent des fleurs et des feuilles".

Charles Babbage mourut ruiné en 1871 et c'est son fils Henry Babbage qui acheva en partie et quelques années plus tard la machine analytique qu'il put rendre opérationnelle. Il en fit don au Science Museum de Londre

En 1991, à l'occasion du 200^ème anniversaire de Charles Babbage, on réalisa une reconstitution d'une machine à différence version simplifiée réétudiée par Charles Babbage lui-même entre 1847 et 1849 mais qu'il n'avait pas non plus eu l'occasion de construire à son époque. Cette machine pèse près de 3 tonnes et est exposée au Science Museum à Londre

Mécanographie

Herman HOLLERITH (1860-1929) mis au point une machine électromécanique destinée à comptabiliser les données recueillies lors du recensement américain de 1890.

La tabulatrice de Hollerith est la première machine qui a utilisé des cartes perforées pour encoder des données. Elle est véritablement à l'origine du traitement automatique de l'information.

Un des rares exemplaires de cette machine est conservé au Computer Museum NAM‑IP à Namur.

En 1896, H. Hollerith créa la société "Tabulation Machine Corporation" qui devint en 1924 "International Business Machine" : IBM

En 1937, George STIBITZ (1904-1995), ingénieur chez Bell Labs, réalisa le premier calculateur binaire électromécanique mis au point à partir de relais téléphoniques et faisant appel à la logique booléenne définie par George BOOLE dans le livre "The Mathematical Analysis of Logic" publié en 1854.

En 1936, Alan TURING (1912-1954) publia dans un article les principes de la machine abstraite qui porte son nom, la machine de Turing, et qui en principe est capable de suivre un algorithme. Pour ce faire, l'unité de commande d'un ordinateur doit être capable de diriger l'exécution du programme qui lui est communiqué sans qu'une intervention humaine ne soit nécessaire au déroulement du programme.

Premiers ordinateurs

L'ENIAC était une machine énorme, elle pesait 30 tonnes et était composée de 18000 tubes à vide. Elle fonctionnait en décimal et non pas en binaire. Chaque chiffre était codé au moyen d'une série de 10 tubes "ring counter" transposition électronique des roues dentées des premières machines arithmétiques. Cette machine était programmée manuellement en positionnant des commutateurs ou en branchant des câbles selon des configurations diverses.

Bien que le tube à vide soit une technologie de type électronique (et non plus électromécanique comme le relais) l'ENIAC ne reprenait ni le principe du calcul binaire du calculateur de STIBITZ ni le principe sans doute encore trop théorique de Alan Turing.

Les plans de l'ENIAC furent terminés en 1944 mais la machine ne fut opérationnelle qu'en 1946.

Dès 1944, les concepteurs de l'ENIAC, déjà en train de préparer furent rejoints par John VON NEUMANN qui rédigea alors un texte présentant le concept de programme enregistré.

Jusque là les programmes étaient lus directement par l'unité de traitement sur la bande ou les cartes perforées introduites à l'entrée de la machine comme cela se faisait dans le métier programmable de Jacquard. Les changements de séquence du programme ne pouvaient donc pas se faire sans intervention humaine. Pour une portion de programme qui devait être répétée il fallait réintroduire à la main la pile de cartes correspondantes.

L'architecture de von Neumann

Von Neumann fait remarquer que puisque les instructions sont codées en binaire, elles peuvent prendre place dans la mémoire de l'ordinateur au coté des données. Ces instructions s'exécutent en suivant l'ordre dans lequel elles sont écrites mais il est possible d'imaginer des instructions de sauts de programme qui ordonnent à l'unité de commande de reprendre la lecture des instructions ailleurs en mémoire autorisant de cette manière les ruptures de séquences automatiques, les sauts conditionnels et les boucles de programmes. L'unité de contrôle peut dès lors reprendre une séquence d'instructions et "prendre des décisions" sans l'aide d'un opérateur humain.

La machine de von Neumann est conçue à partir de composants électroniques, c'est une machine numérique et binaire.
Elle est constituée de cinq sous-ensembles :

• Une unité de commande
• Une unité de traitement (arithmétique et logique)
• La mémoire centrale qui contient donc les données ET le programme
• Une unité d'entrée des données
• Une unité de sortie des résultats

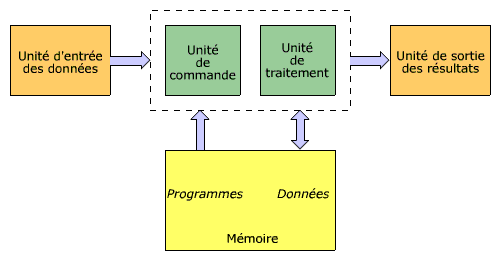
Aujourd'hui encore les ordinateurs fonctionnent toujours sur ce principe. La distinction entre l'unité de commande et l'unité de traitement peut passer inaperçue puisque ces deux éléments sont rassemblés au cœur du processeur. De même, les unités d'entrées et de sorties sont souvent combinées dans les ports bidirectionnels pour être connectés aux périphériques avec lesquels ils échangent des signaux dans les deux sens.