Les additionneurs
Nous allons dans ce chapitre voir comment est en principe construit un circuit pour l'addition de 2 nombres en binaire.
Ce circuit étant assez complexe, nous allons le réaliser en plusieurs étapes :
- Le demi additionneur fera une simple addition de deux bits.
- Le plein additionneur devra ajouter à cette addition celle d'un report précédent
- Enfin nous assemblerons n additionneurs pour faire l'addition de nombres de n bits
Le demi additionneur - half adder
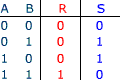
Addition de 2 bits
| S = A xor B est la somme R = A and B est le report |
|
Le demi additionneur effectue la somme de deux bits. S est la somme et R
le report. (carry)
Ce schéma n'est cependant pas suffisant pour réaliser la somme de nombres
de plusieurs bits. Il faut alors tenir compte du report de l'addition des bits précédents.
Le plein additionneur - Full adder
Addition de 2 bits en tenant compte du report précédent
|
Exemple : Calculons 1 + 3 . En binaire cela donne : 0001 + 0011 |
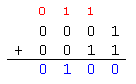 |
L'addition des bits de droite est une addition de deux bits,
elle peut être réalisée avec le demi additionneur.
Pour les bits suivants par contre, il faut tenir compte d'un éventuel report.
Ainsi dès le deuxième bit de notre exemple (en comptant les bits de droite à gauche) il a fallu faire 2 additions ( 1 + 0 + 1 = 10 " on pose 0 et on reporte 1")
Table de vérité et équations et schéma du circuit plein additionneur
Cette table de vérité comporte 3 entrées : R n-1 (le report de l'addition précédente), A et B
Il lui faut deux sorties :
- S = la somme de 3 bits ( A + B + R n-1 )
- R = le nouveau report
Addition de deux nombres de n bits
Exemple : Mise en cascade de 4 additionneurs pour l'addition de deux nombres de 4 bits



